PMF-AMS Analysis Guide
A shortcut to this page is http://tinyurl.com/PMF-guide
The PMF Evaluation Tool (PET) was described in Ulbrich et al., ACP 2009. Please cite the tool with this work in publications in which you have used the PET. The PET consists of several Igor procedure files (ipfs). This wiki serves as the help and documentation for the software. To run PMF with the panel, the PMF executable and associated files, accessed separately, are required (see Section 3, Installing PMF with Igor).
The ipfs were written by Ingrid Ulbrich and Donna Sueper (Jimenez Group, University of Colorado, Boulder) and Greg Brinkman (Hannigan Group, University of Colorado, Boulder). Questions about this code can be addressed to Donna.
PMF (Positive Matrix Factorization) was developed by Dr. P. Paatero (Dept. of Physics, University of Helsinki). Links to Paatero's PMF documentation, including an order form for purchasing PMF from Paatero, and many PMF method papers can be found in Section 9, Other Resources.
This Igor toolkit was intended for use in analyzing AMS data, but there are only few assumptions in the toolkit relating to AMS-type data. Some information on ways to create the necessary waves and matrices from non-AMS data are found in Section 4.1.4, Creating the Data and Error Matrices for non-AMS Users.
Contents
- 1 A Message to Contributors
- 2 Installing PMF with Igor
- 3 Creating the Organics and Error Matrices (Step 0)
- 3.1 Creating the Matrices, by Instrument (Software) type
- 3.2 For AMS Organics + Other Signals including AMS Inorganics
- 3.3 Further Preparation of the Error Matrix
- 4 Perform PMF Analysis *Step 1*
- 5 View PMF Analysis Results *Step 2*
- 6 Compare PMF Results with External Factors *Step 3*
- 7 Considerations for Choosing a Solution
- 8 PMF Evaluation Tool Software
- 9 Other Resources
A Message to Contributors
We want to encourage active participation by all users in the evolution of the information contained within this wiki and welcome the addition of content that is beneficial to the community as a whole. However, please DO NOT delete any content from this page!! Significant time, effort, and deliberation has gone into the information contained in this page. Rather than deleting content, please feel free to voice your concerns by posting a comment to the discussion page where others can contribute (please be sure to include a topic to be referenced in responses).
Installing PMF with Igor
PMF and Operating Systems
The PMF executable is compiled only for Windows/DOS. The PET has generally been tested using Windows 10 and older operating systems Windows XP and Windows Vista. It should run well on either platform; please contact Donna if you suspect you have operating system problems with the PET.
For users with Macs, two options have proven successful. One method is to execute PMF on a Windows computer and then analyze the experiment on a Macintosh. The other method is to execute PMF under the Windows emulator on a Mac. Note that in this latter case, you may need to have the PMF executable somewhere in the c:\ directory; this isn't necessary when running Windows on a PC.
Setting up PMF on Your Computer the First Time
(The BareBones version is currently out of date. You can skip the BareBones version and install the full version of PMF.)
Setting Up the Full Version
After you have confirmed that PMF and Igor interact correctly on your computer with the BareBones version, you are ready to use the full version for analysis.
- Download the .ipf (or .pxt) files from the software section of this wiki.
- Create a new folder on your computer where you'll store the PMF files and all files output by PMF (this should NOT be the folder where you store your Igor experiments). This folder must contain:
- a version of the PMF executable file (obtained from P. Paatero or the BareBones Starter Kit, see also an important note about PMF2.exe files)
- mypmft.ini (obtained from the software section of this wiki)
- pmf2key.key (obtained from P. Pattero, U. Helsinki)
- Start a new Igor experiment and load the 3 .ipf files or load the template. Create your data and error matrices, load them to your experiment, and then proceed to the PMF analysis.
- If there are problems executing PMF, follow the steps for what to do If PMF does not Run Properly to correct the problem.
If you are using PET version 2.04 or lower with Igor 6.21 or higher
Users are encouraged to upgrade their Igor applications to Igor 6.37 or higher, it is free with any version of Igor 6. For completeness, there are some issues with older 6.x versions detailed below. There are two small issues with using old PET versions with Igor 6.21 or higher. You may get an error when Igor tries to compile the pmf code at this line
MoveWave $ThisWvNm, :noNaNs: $NewWvNm
If this is the case, simply change the code to be
MoveWave $ThisWvNm, $":noNaNs:"+NewWvNm
Secondly, when you runPMF with your selected choices (the gold 'Begin PMF analysis with these choices' button), the code perform some calculations on the PMF results that have been loaded into Igor. An error message "StatsRankCorrelation Test error; Does not support Nan or INF" may appear. It is safe to ignore this error and continue. Press the green right-pointing arrow or the Continue button.
It is recommended that one puts all the PMF executable-related files (*.exe and *.ini and *.key etc) in one folder, perhaps named 'PMF_executable', for which you never add or remove other files (except those done automatically by PMF or PET). This PMF_executable folder does not have to be in the 'Program' folder on windows machines; in can reside in within a user's 'Documents' folder. It also should not reside in the Wavemetrics folder or any Igor Pro folder. The location of the Igor template experiment should also not be within the PMF_executable folder.
Important Note about PMF2___.exe Files
PMF executable files are available from P. Paatero in versions that have been compiled for different operating systems. Executable file names that include w are complied for Windows.
At the present time (Nov. 1 2009) all versions of PMF2___.exe are believed to work with the PMF Evaluation Tool. It is important to use the file mypmft.ini for v2.03 or later with files such as pmf2wopt.exe. These newer .exe files check the maximum line length defined in the .ini file, which the old .exe files did not seem to do.
- In the headers of the PMF_Execution_v2_03.ipf (and later versions) file, check these lines for the .exe file you have:
strconstant PMF_EXEC_FILE_NAME="pmf2wtst.exe" //strconstant PMF_EXEC_FILE_NAME="pmf2wopt.exe" //imu2.03 NOTE that if you use this line, you need to upgrade your .ini file to v2.03!!
If PMF does not Run Properly
0. Make sure that the path to the executable is correct. If red text appears in the section 'PMF Executable File Path' then something is wrong. Look in the folder you created with the PMF2wtst.exe or pmf2wopt.exe file. If necessary go to the tab entitled "PMF defaults and advanced options' and reselect the executable file; then go to the run tab, 'PMF Executable File Path' and reselect the folder with your chosen .exe file.
1. Look in the folder you created with the PMF2wtst.exe or pmf2wopt.exe file for the existence of the files
Matrix.dat and StdDev.dat
- If these files exist, Igor was able to access the correct folder. Continue with Step 2.
- If these files do not exist, Igor was not able to access the correct folder. Go back to the first button on the panel and check that you've given the correct path to the folder with the PMF2wtst.exe file. Run PMF again by pressing the second button.
2. Look in the folder you created with the PMF2wtst.exe file for the existence of the file
PMF2.LOG
- If this file does not exist, PMF was not run in this folder. Go to step 3.
- If this file does exist, PMF attempted to run in this folder. Open the file PMF2.LOG (it is a text file).
- Glance down the contents of the file and look for many lines of sequential numbered output, such as
1 rank1 step chi2= 9282.6 Penalty= 1.5287E+04 Flags GF 2 rank1 step chi2= 7411.7 Penalty= 1.4084E+04 Flags GF
- If these lines are in the file, PMF ran successfully on your computer, which must be fast enough to run this data in less than 1 second. You're done! Everything works and you can proceed with real data.
- If the lines of sequential numerical output are not in the file, you should find the following lines within this file (note that every line is NOT included here, but the lines selected here are in the order they appear in the file):
2a)
##PMF2 .ini file for: IMUPMF.INI --- BareBonesPMF Successfully read task initialization file imupmf.ini titled: ##PMF2 .ini file for: IMUPMF.INI --- BareBonesPMF
- If these lines appear in the file, PMF found the .ini file. Continue with Step 2b.
- If these lines do not appear, you should see a message about not finding an appropriate .ini file.
- Make sure that this folder contains the file imupmf.ini, provided with the BareBones PMF Starter Kit. If it did not, copy the file to this folder, delete the file PMF2.LOG and press the second button in the panel again to see whether PMF runs successfully.
- If the file imupmf.ini already exists in the same folder as the PMF2wtst.exe file, continue with Step 3.
2b)
Successfully opened input file 30 with name MATRIX.DAT Successfully opened input file 31 with name STD_DEV.DAT
- If these lines appear in the file, everything should have run correctly. Look at the rest of the PMF2.LOG file to see whether other errors are reported. If you still encounter difficulty, contact Ingrid for assistance and attach the PMF2.LOG file to your email.
- If these lines do not appear in the file, you will see a message about PMF not being able to access one of these files. Check that the files are not being used by other programs, delete the file PMF2.LOG, and press the second button on the panel again to see whether PMF runs successfully.
3. Look in the C:\ directory of your computer (C:Documents and Settings\...\My Documents with the full version) for the existence of the file
runpmf.bat
- If this file exists, Igor was able to write to your C:\ drive. Continue with Step 3a.
- If this file does not appear, Igor was not able to write this file to your C:\ drive. This might be due to high security settings on your computer. You should create a text file with this name (NOT runpmf.bat.txt) and choose to edit it (not open it) with a text editor (e.g., Notepad, WordPad, Emacs, etc.). The file should contain the lines
cd C:\Documents and Settings\Ingrid Ulbrich\Desktop\ pmf2wtst imupmf
- NOTE that you must change the path in this example to the path to the folder where you have put the file PMF2wtst.exe!
3a) Execute runpmf.bat by double-clicking on its icon. You should see the black DOS window pop up, scroll output, and close again.
- If this happens, PMF has run successfully from the batch. In the Igor experiment, press the second button on the panel to see whether PMF runs successfully.
- If the black window does not show scrolled output, continue with Step 3b.
3b) You now need to execute PMF from the command line.
- To access the DOS command line, launch the Command Prompt from your Windows Start menu, located in
Start -> Programs -> Accessories -> Command Prompt
- Change from the path displayed in the prompt to the folder where you put the PMF2wtst.exe file. Use the command
cd
- to change directories (e.g.,
cd Desktop\PMF
- ). You can change one directory at a time, or several at a time as shown in the example. To move up 1 directory, use
cd ..
- Be sure that the folder contains the three files
PMF2wtst.exe (obtained from Paatero or the BareBones Starter Kit) imupmf.ini (obtained from the BaseBones Starter K pmf2key.key (obtained from P. Pattero, U. Helsinki)
- by listing the contents of the current directory, using the command
dir
- Then type this command at the prompt to run PMF:
pmf2wtst imupmf
- You should see scrolling output in the command window. The window will not disappear and you can scroll back through the output (which is also saved in the file PMF2.LOG).
- If the output contains many lines of sequential numbered output, such as
1 rank1 step chi2= 9282.6 Penalty= 1.5287E+04 Flags GF 2 rank1 step chi2= 7411.7 Penalty= 1.4084E+04 Flags GF
- PMF ran successfully here. Delete the file PMF2.LOG and in the Igor experiment, press the second button on the panel to whether PMF runs successfully from Igor.
- If the output does not contain these lines, go back to Step 2 of this section to examine errors that might be reported by PMF in the file PMF2.LOG.
Creating the Organics and Error Matrices (Step 0)
Creating the Matrices, by Instrument (Software) type
- The Igor AMS PMF tool needs 4 inputs: two 2-dimensional matrices of the same size and two 1-dimensional waves corresponding to indexes of the rows and columns. One 2-dimensional matrix is the organics matrix (typically PMF is only performed on organics), the other is the error of the organics matrix. The Igor PMF code also needs two 1-dimenensional waves corresponding to index values for the rows and columns of the data matrix. These are the times series (corresponding to the rows) wave and a m/z wave (corresponding the columns).
- Regardless as to whether the data has been generated from a quadrupole or tof ams, user should select the use MS airbeam correction option for generating the organic matricies. This is because the error matricies will be generated using the airbeam correction factor if it exists.
- Some steps are slightly different between manipulation of the quadrupole and the tof ams data sets. In the quadrupole the removal of spikes and the smoothing of data may be necessary, where as in the tof data sets, neither may be required (due to the fact that the quadrupole only samples one m/z at a time).
- Note that the data itself need not be strictly non-negative. The PMF executable and PET procedures will work fine if the data matrix has negative values. The error matrix, of course,, should have only postive.
In the Q-AMS Software (James')
- Be sure to use v1.41 or later of the Q-AMS Analysis Software ("James' Program"). Corrections have been made since earlier versions to the error calculation routines!
- Download from Qi Zhang's website Extract Waves&matrices v 1.1.ipf (note that v1.2 is for Squirrel/HR data) and include it in your experiment with James' software.
- Call org_mats, which will calculate a data matrix (organics_MS) and error matrix (organics_MS_err) in root: in your expeiment, and save these matrices along with the timeseries for organics, sulfate, nitrate, ammonium, and chloride in a file called "WavesMatricesForOrganicAnalysis.itx" (Igor should prompt you for the folder where you want to save the data). All of the data are saved in ug/m3 with all corrections (CE, RIE) applied.
- You may want to load the saved waves into a new experiment to run PMF.
- You'll also need to include your time series wave (t_series) and a wave of the m/z's in the matrix (amus).
Continue to the Deleting NaNs/zeros for all Instruments section
Recommended Practice: Removing Spikes
"Spikes" in the time series of an m/z can occur in Q-AMS data from large but infrequent particles during the scanning of the quadrupole. If such spikes have a common source with a factor that can be retrieved by PMF, they may increase the variation of that factor profile and additional factors may be found that represent this variation, but not a physically-meaningful, separate component. The "excess signal" from these spikes can be subtracted from the spikes and the average mass spectrum of the spikes examined. See Zhang, Q. et al., ES&T, 2005.
Note that if you remove "excess signal" in the method of Zhang et al. 2005 and leave the error values for these points unchanged, you are automatically "downweighting" these points in PMF. This is appropriate because the replacement value for the original spike is not known as well as the values for points without spikes.
Optional Practice: Smoothing
Smoothing can be used to reduce high-frequency noise in the data that could also be fit as additional factors. If you smooth the data, be sure to propagate this smoothing in the error matrix (not added to the wiki yet).
Continue to the Deleting NaNs/zeros for all Instruments section
In SQUIRREL
- In squirrel the main two data sets containing the unit resolution sticks and unit resolution errors are MSSDiff_p and MSSDiff_p_err. These data sets may reside in the root folder or may reside in intermediate files, depending on the version of squirrel and the settings chosen by the user. The code within squirrel will automatically retreive these data sets as needed.
- If the error matrix has not yet been calculated, this must be done first. In the Corrections tab, Errors sub-tab, check the calc MS errors checkbox. Make sure you don't intend to do any other calculations (such as creating a new AB correction factor) in the corrections tab and then press the Do Corrections button. This will generate the MSSDiff_p_err data set.
- Squirrel verions 1.46 - 1.48
In these versions the creation and export of the waves needed for PMF analysis is performed in several steps.
- The squirrel interface for generating the Org and Org error matricies in Squirrel have changed slightly before and after version 1.46 - 1.48. In all versions one goes to the MS tab, average mass spectra section, enters (only) Org as a species. In versions 1.46 and higher one needs to check the 'Calc, plot 1sigma err' checkbox and optionally use the 'Prompt for max m/z' checkbox and then press 'Calc Time Series Spectra' button (v. 1.47+).
- In versions 1.46 and lower one uses the 'Export Matrices' button. After the operation is finished the matricies you need will reside in the root folder: MSSD_xxx_Mat_Org and MSSD_xxx_Mat_Org_err (v. 1.46 and lower) or MatD_xxx_Org and MatD_xxx_Org_err (v. 1.47) where xxx is the name of the todo wave. Both of these matricies will have zeros in the m/z columns where no organics contribution is identified (as is given in the frag_organics wave) and blanks in the rows for run numbers not included in the todo wave. In the case of version 1.46 and lower, the MSSD_xxx_Mat_Org_err will not be calculated unless MSSDiff_p_err has first been created.
- Now you have the two most important basic pieces - the Org matrix and the Org error matrix.
- The two 1-dimensional waves corresponding to the rows and columns of the matrix are the time series wave and a simple wave corresponding to m/z. In squirrel the time series wave is root:index:t_series. There is a m/z wave, root:diagnostics:amus whose values are simply column numbers, 1,2,3,...1000. This is the wave that is plotted as the x axis when one generates and average mass spectrum. For simplicity, the maximum value is always 1000, regardless as to what the maximum m/z data value is. Users can either redimension this amus wave to be the correct size (the same number of points as the column of the data matrix) or to create a new wave simply by the command line.
- There is still more work that needs to be done: calculating the minimum error, removing columns with zeros/nans, and perhaps doing some editing on the error matrix. Continue to the Deleting NaNs/zeros for all Instruments section
- Squirrel verions 1.49 and higher.
In squirrel version 1.49 and higher a new checkbox 'itx for PMF' appeared next to the 'Calc 2d matrix' button. Since almost every time a user wishes to create the full Org time series spectra, this checkbox was added to streamline this process.
- When the 'itx for PMF' checkbox is checked the code will check to ensure that only one species is selected: Org. It will also check to ensure that the error checkbox is checked, as one needs both the signal and the error matricies for pmf. Lastly, it checks that the AB correction factor has been checked, as the errors were calculated using the AB correction factor wave.
- After pressing the '2d time series spectra, a prompt will appear asking the user for the maximum m/z range to use. It is typical for ambient organic signal that a maximum of m/z of approx. 300 is used for pmf, but the user can request to export up to the maximum m/z range acquired if they desire.
- Along with the signal and error matricies, the minimum error will be calculated.
- All waves needed to begin the PMF analysis preparation will be created and exported to a itx (igor text file) in a location of the user's choosing. These waves include the 2-d signal wave called OrgUg or OrgHz, 2-d error wave called OrgUgErr or OrgHzErr, the t_series wave, the amu wave, the minimum error wave (in the same units as the data and error wave), and a rn_series wave. The rn_series wave is not needed for PMF analysis but is included for possible reference use.
- It is important to know that the RIE and CE are *NOT* applied to the Org and Org error matrix if you choose unit so ug/m3. The general convention is that whenever Squirrel outputs anything with an m/z dimension the units are NO3-equivalent. The thinking behind this convention is that whenever we have an m/z dimension, such as with an average mass spectra, we want to be able to sum the unit resolution sticks to get back to the unspeciated signal an any nominal mass.
In PIKA
Please use the latest version of Pika. Since version 1.14 and higher a button exists for preparing and generating matricies for input into PET. The comments below reflect early conditions of Pika and should no longer be considered relevant, unless you are using an old version of Pika.
Pika has evolved rapidly between 2008-2010, and generating the High Resolution stick matrix in Pika will depend on the version you are using.
Pika 1.13
- A document describing the methodology and the calculations for HR errors was created in May, 2014.
Pika 1.08 and higher
The interface and behavior for generating in memory HR sticks and errors is very similar to that in Squirrel.
As in the case for Squirrel, the Igor AMS PMF tool needs 4 inputs: two 2-dimensional matrices of the same size and two 1-dimensional waves corresponding to indexes of the rows and columns. However in Pika one will typically want two 1-dimensional waves describing the HR ions within the columns: one indicating the mass value (i.e. 12.000) and one indicating the chemical formula (i.e. C etc).
There is a button in the HR Results tab in the lower left corner titled "Calc time series spectra (2d matrix, not plotted, leave list blank for all HR ions)". Most AMS users will want to analyze the HROrg species, so include this item in the control for selecting the results (right under "Step 6. "). From the drop down menus, most will want to choose the OMinusC data type, check the Calc, plot err. checkbox, and select the OMinusCIonCountErr error type. When the user presses the "Calc time series..." button a 2-D data matrix called called HRMxM_HROrg (or HRMx*) and a 2-D error matrix called HRMxM_HROrg_err (or HRMx*err) will be generated.
HR data and error matrices will have the number of rows equal the the root:index:t_series wave, just like in squirrel. Rows will have nan values for runs not in the todo wave selected. If the HROrg species was selected (typical), all calculations in the HR batch table and HR_frag_organic have been applied to both matricies, just as in squirrel.
Whereas in squirrel matrix columns correspond to integer m/z values (column 0 = m/z 1 etc), for high resolution spectra, columns correspond to individual HR ions. So if the first three HR ion fit were C, j13C, CH, then the first column is C, the second is j13C, the third is CH, and so on. If an HROrg matrix was generated there may be column for HR ions that were not fit but were included in the HR frag table, such a S j33S, etc. The text and numeric waves of HR ions corresponding to the columns are root:HR_frag:SpeciesMassText and root:HR_frag:SpeciesMassWave. For users of 1.90+ a button called "HR ions for HR species table" will bring up these waves in a table for you. You will often want to export two waves to indicates HR column values - one containing the exact mass values (12.00000, etc) and one containing the HR ion chemical name (C, etc).
In Pika 1.09F there is a handy checkbox that when checked will automatically generate an itx containing all the waves necessary for the PMF (with the exception of any data preparation steps such as the minimum error, Nan removal, etc.)
- It is important to know that the RIE and CE are *NOT* applied to the HROrg and HROrg error matrix if you choose unit so ug/m3. The general convention is that whenever Squirrel or Pika outputs anything with an m/z dimension the units are NO3-equivalent. By using nitrate equivalent mass, we are scaling all ions equally (i.e. not scaling differently according to which species each ion contributes to). This means that the mass spectra in ugm3 units are identical to those in Hz units except for a single scaling factor. The thinking behind this convention is that whenever we have an m/z dimension, such as with an average mass spectra, we can sum the unit resolution at any nominal mass to compare to the unspeciated signal.
For AMS Organics + Other Signals including AMS Inorganics
Setting up the signal and error matricies for org+inorg is not terribly difficult. The interpretation is much more complicated and nuanced than for a PMF analysis on only the organics. More on this in the * and ** sections below.
Adding other signals to the organic matrix and error matrix is done most simply by a cut and paste operation. In Igor make 2 tables:one containing the organic matrix, the other containing the error matrix. You will cut and paste columns (columns correspond to the time series in the 2D matricies) to the organic and error matrices. In the case of UMR you will likely have to add new columns to the organic matrix to the right side end, the max m/z, and keep track of which columns indicate which species m/z. This is because, for example, m/z 30 will have independent signals from org and nitrate.
Below is instructions for nitrate, do the same for any other inorganics you wish to use.
For UMR:
Get the UMR inorganic species signal and error matrix from the squirrel panel just as you would for Org. Look at the frag table and find which UMR values correspond to 'underived' nitrate signal - for nitrate it is m/z 30 (NO) and m/z 46 (NO2). Everything else in frag_nitrate is a linear multiple of these two signals. At this point you have two options for your cutting and pasting. There exists an org and a nitrate signal at m/z 30, so our m/z X = columnX-1 system will be messed up. I suggest that you simply copy and paste the nitrate signal at m/z 30 and 46 to the max org m/z signal you have. So if your original org matrix had 200 columns corresponding to m/z 1 - 200 (columns 0 - 199), your new organic+nitrate matrix will have 202 columns.
The PMF tools won't care at all that column 200 (counting from zero) really is nitrate at 30, etc; it will execute fine. However, you will have to get used to looking at these modified 'spectra' in the pet panels. When you get ready to publish this, you will have to modify/separate out 'by hand' the org and nitrate parts and 'fold in', if you like, the UMR derived portions of your nitrate signal (i.e. 0.004*frag_nitrate[46] at m/z 48 for nitrate).
For HR:
The m/z columns in the HRorg matrix corresponds to individual HR ions so the copying and pasting of columns will be much more intuitive.
You can create the HRNO3 matrix as you did with HROrg and and copy and paste the NO and NO2 columns into the HROrg matrix, overwriting the columns of zeros you have for the organic matrix NO and NO2 columns. It is much easier all around if, when you create your HROrg matrix, you do not include constrained isotopes, because the downweighting of these duplicate signals is tedious.
Now repeat for all other HR ions in the NO family, perhaps NO3 or HNO, etc, depending on what HR ions you chose to fit. I will assume that any CHNO ions do not have a N-O bond and are thus considered to be 'organic' and not 'nitrate'. These signals, if they exist, are likely very small and I doubt that they would cause problems, but users should be aware of any of these types of assumptions they are making.
Another option would be to create time series of all the NO family ions and do the copying and pasting of these values. A benefit of doing it this way is because the HRNO3 matrix will be huge and almost entirely filled with nans. The downside to this option is that whenever you chose to plot a time series of a single HR ion like NO, *no RIE or CE is applied*. So you can manually multiply these HR ion time series waves NO_blah by the correct RIE and CE before you copy and paste into the HROrg matricies.
Considerations:
- Which brings me to the RIE and CE issue. PMF is sensitive to relative contributions of your signals; I believe (Manjula can correct me) that you may have to tweak the inorganic signals by a multiplicative factor (i.e. 0.9 or 1.1 or some such) in order to get PMF factors that believably separate or blend with any organic signals.
- A small but tedious detail to be aware of is the H2O contributions for sulfate and organics. If you do an organic+sulfate+xx PMF analysis I'd just remove all signals of OH and H2O (and O?). We estimate these HR ion contributions from the major signals (CO2, etc) anyway.
For non-AMS Users
You will need to create 5 waves to run your PMF analysis in Igor:
- a data matrix
- an error matrix
- a text wave that has the names of your species (short names are better)
- a numeric wave that has index values for your species (1, 2, 3, ...)
- a time wave
This section describes how you might make those waves, assuming your data is in Excel and is loaded to Igor with one wave for each species and another wave for each species' error values. Depending on the initial format of your data, some steps may not apply to you.
Loading data from Excel into Igor
In Igor, go to the Data pulldown menu and choose Load Waves -> Load Excel File... (Note that the Excel file must be closed when you try to load the waves.) You can choose the wave names based on column headers from the Excel file if you wish. Note that you can probably uncheck "Make double precision waves."
If your Excel file has data values in one sheet and error values in another (especially if the columns have the same titles), you may wish to load all of the data waves in one datafolder and all of the error waves to another datafolder and form the data and error matrices in these locations.
Note that in Igor you cannot use a digit as the first character in a wave name, nor may you use operators (+ - * / ? etc.) or spaces in wave names.
Concatenating 1-D Waves to form a 2-D matrix
You will use Igor's concatenate function to make the 1d waves into a 2d matrix. This is easiest to do with a "wavelist" -- a string that contains all of the relevant wave names, separated by a semicolon (the default separator in Igor). For example,
string/G SpeciesWaveNameList = wavelist("", ";", "")
will make a string called SpeciesWaveNameList with a list of all of the waves in the current folder. You may wish to check that all of the wave names are correct in the string. You may need to remove any wave names from the list that you don't want to include in the matrix (e.g., year). This can be done by a line like
SpeciesWaveNamesList = removeFromString("year;month;day;PM10;", SpeciesWaveNamesList)
Now you can make the matrix by
concatenate SpeciesWaveNameList, DataMx
When you do this for the error matrix, be sure to check first that the strings in the data and error folders are identical so that all species are included in both waves in the same order!!
Making a Text Wave of Species Names
The SpeciesWaveNamesList can be converted to a text wave using a function in the Igor PMF software (so these .ipf's must be loaded in the experiment:
gen_list2txtWv(SpeciesWaveNamesList , "SpeciesWaveNames")
The wave of species names is now called SpeciesWaveNames. (You'll only need to do this once, since the list is the same for the data and error waves.)
Making a Numeric Wave of Species Indexes
You can create a numeric wave with indexes counting from 0 by
make/N=(numpnts(SpeciesWaveNames)) SpeciesWaveIndex = p
(Note that "p" is an Igor convention for indexes. You can count from 1 by changing "p" to "p+1".)
Making a Time Series Wave
Igor has its own convention for time, counting in seconds from 1/1/1904. Because this creates very large numbers, time waves should be double precision (/D flag). Two examples for making time waves are shown here.
For daily data, with input waves year, month, and day:
make/N=(numpnts(year))/D timeseries = date2secs(year,month,day)
For data with input waves year, month, day and also hour, minute, and second:
make/N=(numpnts(year))/D timeseries = date2secs(year,month,day) + hour*60*60 + minute*60 + second
Further Preparation of the Error Matrix
The following steps are recommended for AMS datasets and follow the practices laid out in Ulbrich et al., ACP, 2009 (with more detailed references in each section below). Note that the only mandatory step is Deleting NaNs/zeros. The functions for the error modifications can be found in pmf_ErrPrep_AMS_v2_3.ipf. More extensive documentation on use of the functions is given in the headers in that file.
Before running these functions, you should duplicate your error matrix and give it a short name (fewer than 12 characters). Each function lengthens the wavename and the functions will complain if the name gets too long.
Recommended Practice: Set a Minimum Error
Ions arrive at the mass spectrometer detector with a Poisson distribution. The error for a counted number of ions is sqrt(counted number of ions). The smallest number of ions we can count in one run is, of course, zero ions, but perhaps there was one and it was missed. The error for counting zero is sqrt(0), but an error of 1 would be more appropriate in this case. Hence a minimum error threshold of 1 ion is set.
Within this step the user must choose the mass spec detector type. For ToF detectors, there is an m/z dependence to account for the unequal 'pushing' of the ions into the detector. Small m/z ions move faster than large m/z at an approximate rate of square root of the mass. This phenomena is sometimes referred to as an 'm/z duty cycle' correction. The application of a minimum error must undo this duty cycle correction if it was applied to the data to reflect true ions counted. In practice then, when one selects the AMS-ToF for the MS type, a sqrt(28)/sqrt(m/z) factor is temporarily multiplied to the error matrix. For AMS-quad data and for tofware-processed CIMS data, this undoing of the correction factor is not needed.
The one ion wave needs to be in the same units as the data and error matricies. If the data and error matricies are in units of Hz and the data acquisition (the actual time measuring i.e. in the 'MS open' mode) for each run is 1 second, then the one ion wave is simply a wave containing all 1s. If each run had an MS open mode lasting one minute, the wave would consist of 1/60. If the data and error matricies are in typical AMS units of ug/m3 then one needs to convert from Hz using the flow rate, ionization efficiency, AB correction factor, etc.
The minimum error is applied in three steps:
- In the experiment with James' panel or Squirrel, calculate the signal equal to 1 ion with the function pmf_err_minErr1ion_ugm3 in pmf_ErrPrep_Q-AMS_OneIonEquiv_v2.3.ipf or pmf_ErrPrep_ToF-AMS_OneIonEquiv_v2.3.ipf. This function operates on the current todo wave.
- Copy the wave minErr1ion_ugm3 or minErr1ion_Hz (depending on the units of your matrix) into your PMF experiment.
- Run the function 'pmf_err_errMx_minErr (found in pmf_ErrPrep_AMS_v2_3.ipf), using your error matrix with the short name.
The function produces the following waves:
- The error matrix with minimum error applied called nameOfWave(errMx)+"_min" (e.g., OrgMSerr becomes OrgMSerr_min)
- A matrix of the fractional increase of the errors called nameOfWave(errMx)+"_adjErrMask" where the value of each point is (new/old)-1.
See also discussion of Ulbrich et al., ACPD 2008, P. Paatero comment (p. S5730) and Author response (p. S11960)
Propagation of Smoothing (when relevant)
Any smoothing of the data matrix must be propagated in the error matrix. The function pmf_err_propogateSmooth propagates box or Gaussian smoothing.
Some notes about specifying the smoothing that was performed for the data:
- Allowed types of smoothing are "box" and "Gaussian".
- The type of smoothing that is done in the AMS software is selected in the Misc tab.
- The number of points used in box and Gaussian smoothing is used as defined in Igor.
- For box smoothing, the number of points refers to the size of the box. I.e., smoothing that includes 1 adjacent point on each size is 3-point smoothing.
- For Gaussian smoothing, the number of points refers to the number of adjacent points used. I.e., smoothing that includes 1 adjacent point on each side is 1-point smoothing.
The function produces a wave with the propagated error called nameOfWave(errMx)+"Prop" (e.g., OrgMSerr_Min becomes OrgMSerr_minProp).
Deleting NaNs/zeros for all Instruments
The matrices produced in the previous steps have NaNs in all rows from bad runs and 0 values in columns with good runs that have no organic fragments. All of these rows and columns need to be removed before running PMF. This is a two-step process.
1. First, change the columns with 0's to NaNs.
1a. You can do this by changing all 0's to NaNs, e.g.
- OrganicMx = OrganicMx[p][q] == 0 ? NaN : OrganicMx[p][q]
OR
1b. you could make an organic fragments mask wave (= 1 for organic fragments, = NaN for others) and multiply your matrix by the wave. This is also a good time (and easy way) to delete other columns you way not want to retain in the PMF analysis (e.g., m/z's 19 and 20, which are small copies of m/z 44 in the normal frag table).
Note that 1b is safer because of the way this function works (see Important Note below)! If an actual good data value in the first row was 0 (unlikely but possible) and you have replaced zeros by NaNs, a column may be deleted inadvertently!
2. In the PMF_Execution_XX.ipf, use the function
- pmf_ams_deleteNaNs_mxWvs(dataMx, errMx, rowDescrWv, colDescrWv)
where
- dataMx and errMx are your data and error matrices,
- rowDescrWv is a 1-D wave that gives the indices for the rows (usually t_series), and
- colDescrWv is a 1-D wave that gives the indices for the columns (usually amus).
The function creates new versions of the input waves with names noNaNs_amus, noNaNs_t_series, etc. from which the NaN rows and/or columns have been deleted. 2-D waves called NaNsWv_amus and NaNsWv_tseries have been created and are used by related functions to delete items from other waves or reinsert the original NaNs into waves. (Note: NaNsWvs were stored as NaNsLists before v2.03.)
3. Check whether any NaNs remain in the matrix. (This may happen with HR data where the fit returned NaN for a particular peak.) You must replace any NaNs with some value and choose an accompanying error value. It is imperative that you describe how these values were handled and how many values were effected when publishing results! (People who have addressed this issue are encouraged to add to the recommendations in this section!)
Considerations for Replacing NaN Values
- These values are suspected to be equal to or close to 0. Zero values are allowed in the PMF input, but cannot actually be fit as zero. Very small positive values are probably a better choice than zero.
- Read and evaluate other studies performed with PMF. This issue is more common in filter datasets than in AMS data and several practices have been developed for dealing with below detection limit and missing values in these dataset. Consider whether the practices in the literature are appropriate for AMS data.
Considerations for Setting Uncertainty Values for Replaced NaNs
- The uncertainy of the replaced NaN value should be estimated from the uncertainty of that fragment.
- The estimated uncertainty for the replaced NaN value should be increased by a factor of ~100 so that this point has almost no weight.
- As above, read and evaluate other studies performed with PMF and consider whether practices in the literature are appropriate for AMS data.
Important Note about Using DeleteNaNs Functions!!
The pmf_ams_deleteNaNs_mxWvs function chooses the first row and column of the data that contain a mix of NaNs and values and uses this as a template to delete rows or columns (respectively) that contain NaNs. It does not check every single value in the matrix. This is because there should not be any nans or infs in the matrix unless there are nans or infs in the entire row or column. After running this function, it may be wise to check (e.g., with wavestats) whether all NaNs have been removed.
Here is a piece of code that can remove columns with zeros. This approach presumes you have already used the pmf_ams_deleteNaNs_mxWvs function above.(Copy and paste these lines into a procedure window and execute from the command line.)
// A function for removing columns in a matrix that have only zeros // For example, if a user has an "Org" matrix, it would remove columns // corresponding to m/z 1 - 11, 14, etc. // sample usage: RemoveZeroCols(noNaNs_mx, noNaNs_mxerr, noNaNs_amus, NaNsList_amus) // where noNaNs_mx and noNaNs_mxerr are replaced with your wave names Function RemoveZeroCols(noNaNsmx, noNaNsmxerr, NoNansAmuWave, NoNansAmuList) wave noNaNsMx, noNaNsMxErr, NoNansAmuWave string NoNansAmuList variable idex, numRow, numCol numRow = dimsize(noNaNsMx,0) numCol = dimsize(noNaNsMx,1) make/o/n=(numRow) tempCol for (idex = numCol;idex>=0;idex-=1) // work 'backwards' so that we don't mess up the counting tempCol = noNaNsMx[p][idex] wavestats/q/m=1 tempCol if (V_min ==0 && V_max == 0) deletepoints/m=1 idex, 1, noNaNsMx, noNaNsMxerr deletepoints/m=1 idex, 1, NoNansAmuWave NoNansAmuList = num2str(idex+1) + ";"+ NoNansAmuList// keep adding at the front to keep in numerical order. endif endfor killwaves/z tempCol End
Related Functions
Also found in PMF_Execution_XX.ipf:
- pmf_ams_deleteNaNs_Wvs(wvList, NaNsList)
- Applies the NaNsList_amus or NaNsList_t_series to delete points from any list of waves of the same dimension.
- pmf_ams_deleteNaNs_Mxs(wvList, NaNsList, NaNsDimension)
- Applies the NaNsList_amus or NaNsList_t_series to delete points from any list of matrices in the specified dimension (using standard Igor dimensions, where 0=rows, 1=columns). This could be used e.g. to delete the same set of rows or columns from a matrix other than the data matrix (used as the original template) or the error matrix. Not currently available in PMF_Execution_XX.ipf; contact Ingrid if you're interested in this function.
- pmf_ams_insertNaNs_Wvs(wvList, NaNsList)
- Applies the NaNsList_amus or NaNsList_t_series to insert points into any list of waves of the same dimension. This is very helpful for making final t_series waves for publication that don't have lines across periods of no data.
- pmf_ams_insertNaNs_Mxs(wvList, NaNsList, NaNsDimension)
- Applies the NaNsList_amus or NaNsList_t_series to insert points into any list of matrices in the specified dimension (using standard Igor dimensions, where 0=rows, 1=columns).
- pmf_ams_NaNsList_2_NaNsWv(NaNsListName)
- Converts NaNsLists (v. 2.02 and earlier) to NaNsWvs (v 2.03).
- pmf_ams_RemoveBlockSize_NaNsWv(NaNsWv, BlockSizeToRemove)
- Creates NaNsWv_type_trunc and deletes the records for original blocks of NaNs of size BlockSizeToRemove. If you did V-W switching and are only running the V-mode data in PMF, your NaNsWv_tseries will have an entry for every other row of your original matrix noting that 1 NaN row was removed. You may also have periods with longer contiguous runs of NaNs (e.g., instrument was down, filter runs, etc.). For publication plots, you should insert NaNs into your final factor waves so that periods of missing data are not crossed by a line connecting the good data before and after the real gaps. For NaNs removed due to menu switching, however, you may not want to insert all of these NaNs again. (In the example case, each solved value would have a NaN on each size of it and you couldn't plot with Lines Between Points. If you uncheck "Gaps" to connect these points, you'll also have the undesirable lines across periods of missing data.) Running pmf_ams_removeBlockSize_NaNsWv(NaNsWv_tseries, 1) would create NaNsList_tseries_trunc which would not include a record of all the removed W runs and then could be used to insert NaNs representing only missing data periods in the final waves.
Recommended Practice: Downweight "Weak" Variables (m/z's)
Any m/z 's that have low signal-to-noise ratio (SNR) may, in fact, have more noise than signal. If these m/z 's contribute enough Q, PMF tries to fit the noisy data. In this way, the inclusion of such m/z 's can be detrimental to the PMF analysis. If the error associated with these m/z 's is increased, the Q-contribution (residual/error) is decreased, "downweighting" these points' contribution to the fit. m/z 's with SNR<0.2 are considered "bad" by Paatero and Hopke (2003) and should be removed or strongly downweighted (factor of ~10). m/z 's with 0.2<SNR<2 are considered "weak" and should be downweighted (factor of 2-3).
The calculation of SNR and downweighting of "weak" m/z's is carried out in three steps:
- Calculate SNR of each m/z using function pmf_err_SNRwv using the data matrix, the version of the error matrix generated in the previous step, and the model error that will be used in the panel. The function generates a wave of the SNR for each m/z called nameofwave(DataMx) + "_SNRwv".
- Check the graph produced for "bad" m/z's. These are not removed in the next function. To remove these columns, you'll need to rerun the DeleteNaNs step after making them into NaNs or changing them in the mask wave. (This is better than just deleting the columns by had because they'll be added to the NaNsList_amus and will be reinserted if you insertNaNs later.
- Downweight "weak" m/z 's with function pmf_err_DwntWeakColumns using the SNRwv generated in the previous step, the error matrix used to calculate the SNRwv, and the multiplicative value used to downweight the weak m/z 's (Paatero and Hopke recommend 2-3).
The function generates a new error matrix called nameofWave(errMx)+"Wk" (e.g., noNaNs_orgMSerr_minProp would become noNaNs_orgMSerr_minPropWk).
See also Paatero, P., and Hopke, P. K.: Discarding or downweighting high-noise variables in factor analytic models, Anal. Chim. Acta, 490, 277-289, 10.1016/s0003-2670(02)01643-4, 2003. Abstract
Recommended Practice: Downweight Peaks Related to m/z 44 in Frag Table
In the default fragmentation table, the information in m/z 44 is repeated 6 or 7 times (in m/z 's 16, 17, 18, 19, 20, (28 in the Aiken et al. 2008 revision), and 44) with different proportionalities. PMF fits correlations, regardless of the magnitudes of the signals. Repeating the information of m/z 44 several times implies that it's really (x6 or 7) important, which it isn't! It is possible to downweight the columns of these m/z 's so that in total they only contribute the m/z 44 signal once. (It would be possible to remove the repeated information and replace those columns after running PMF, but we think that downweighting them is logistically simpler.)
Downweighting the m/z 's related to m/z 44 is accomplished in two steps:
- Make a wave that contains the m/z 's related to m/z 44 (in any order), e.g.
- make/N=4 mz44peaksWv = {16, 17, 18, 44}
- make/N=5 mz44peaksWv = {16. 17, 18, 28, 44}
- make/N=6 mz44peaksWv = {16, 17, 18, 19, 20, 44}
- make/N=7 mz44peaksWv = {16, 17, 18, 19, 20, 28, 44}
- Use function pmf_err_dnwt44peaks with the error matrix generated in the previous step, the mz44peaksWv, and the noNaNs_amus wave.
The function generates a new error matrix called nameofWave(errMx)+"44" (e.g., noNaNs_orgMSerr_minPropWk would become noNaNs_orgMSerr_minPropWk44).
If you are analyzing HR data and using the default HR organics frag waves, the equivalent set of HR ions of (the mz44list) correspond to O, HO, H2O, CO and CO2.
Perform PMF Analysis *Step 1*
Additional File for PMF Executable Directory
Be sure that the file
mypmft.ini
(provided on the PMF data page) is located in the directory with the PMF Executable.
Recommended Practice: Organizing Your Folders
+ root
+ TemplateData to copy for new versions of analysis
+ Variation1 e.g., your basis case
+ Variation2 e.g., with different error estimates
+ External_MassSpectra for use with the Scatter Panel
+ External_Tseries for use with the Scatter Panel
NOTE: Data for running PMF can be in root: or a subfolder of root: , but not any lower folder.
The Executable Panel
- Set the path to the PMF executable
- Provide the data and error matrices information
- Chose the folder (must be root: or a directory in root:)
- Choose the Data and Error matrices (use noNaNs_ versions)
- Choose model error (PMF increases the errors provided by newError = oldError + modelError*dataValue)
- Choose the type of PMF analysis
- Exploration will run PMF for a range of number of factors and FPEAKs or SEEDs. This is the typical use for exploring a dataset and comparing many solutions.
- Bootstrapping explores the uncertainty of one solution (i.e., one number of factors at one fpeak for one seed). This is usually a final step run only on the solution you have selected from the exploratory analysis.
- Choose a range for number of factors.
- When checking to make sure that everything runs properly, you may want to run just one case (Min p = 2, Max p = 2).
- Recommended Practice: Run cases with 1 factor to have a context for the meaning of the 2-factor solution.
- In the Bootstrapping mode, only the "min p" is read; the "max p" is ignored.
- Choose FPEAK or SEED values
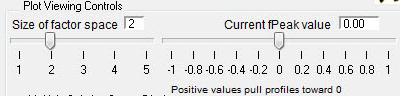
- "FPEAK" is a tool used to explore rotations of the solutions of a given number of factors. Note that FPEAK does not explore all possible rotations of a solution. FPEAK = 0 does not apply any rotational forcing. Non-zero values of FPEAK create near-zero values in the factor profiles (mass spectra) or time series. More information about FPEAK can be found in the PMF Users Manual Part 1 (pp. 9,12,14,21) and Part 2 (p. 24), and in several papers by P. Paatero (see Other Resources).
- A good first set of FPEAK values is -1.0 to +1.0 with a delta value of 0.1 or 0.2. For a full analysis, a wide enough range of FPEAKs to achieve Q/Qexp of at least 1% above the minimum value is recommended.
- In Exploration mode when varying the fpeaks, the Seed is set in headers in the PMF_Execution...ipf file: constant DEFAULT_SEED = 0
- In Bootstrapping mode, only the "min fpeak" is read; the "max fpeak" is ignored.
- "SEED" is a tool used to choose different random starts (initial values) for the PMF algorithm. Using different seeds may lead to solutions in different local minima (Q/Qexp) in the solution space. One set of solutions may have more physical meaning than another, or multiple sets may make physical sense. It is impossible to test all start values, but testing many seeds may give an indication of local minima for your dataset. More information about seeds can be found in the PMF Users Manual Part 1 (p. 11) and Part 2 (p. 16).
- Run seeds from 0 to your preferred maximum with a delta value of 1.
- In Exploration mode when varying the Seed, the fpeak is set in the headers of the PMF_Execution...ipf file: constant DEFAULT_FPEAK = 0
- Exploring Seeds with a non-zero fpeak should be done with caution, as the "push" of a magnitude of fpeak for one area of local minima may be different than the "push" of the same magnitude of fpeak for a different area of local minima.
- In Bootstrapping mode, the Seed is set in headers in the PMF_Execution...ipf file: constant DEFAULT_SEED = 0
- "FPEAK" is a tool used to explore rotations of the solutions of a given number of factors. Note that FPEAK does not explore all possible rotations of a solution. FPEAK = 0 does not apply any rotational forcing. Non-zero values of FPEAK create near-zero values in the factor profiles (mass spectra) or time series. More information about FPEAK can be found in the PMF Users Manual Part 1 (pp. 9,12,14,21) and Part 2 (p. 24), and in several papers by P. Paatero (see Other Resources).
- Select checkboxes
- Run PMF in background Each execution of PMF (see Exploration Mode Summary) creates a black DOS window that pops up. If the box is not checked, this window "grabs the focus" and makes itself the top window. This makes it hard to use the computer for anything else. If the box is checked, the window will not grab focus, but Igor and your computer's CPU will be busy.
What the Software Does When You Press the Button...
Exploration Mode Summary
The software will execute PMF once for every combination of number of factors and FPEAK/seed. So if you run 1-5 factors and 5 FPEAKs, PMF will run 5x5=25 times. Each run starts a new black DOS window that will close when the run is completed. The duration of each run is printed in the history at the end of each run. In general, runs which solve for more factors and runs with FPEAK farther from 0 take longer. The code runs all of the FPEAKS or seeds for one number of factors, then advances to the next number of factors (e.g., run 1 factor with each of 5 FPEAK values, then 2 factors with each of 5 FPEAK values, etc.).
A little more detail
The software writes the files
C:\delete_log.bat C:\runPMF.bat
and writes your DataMatrix and ErrorMatrix as MATRIX.DAT and STD_DEV.DAT, respectively to the folder with your PMF Executable. The software also writes a file to that folder called STD_DEV_PROP.DAT, which has the same number of points as the DataMatrix and in which every element is equal to the ModelError.
The software then enters a pair of nested loops in which the following steps occur:
- for each number of factors
- for each FPEAK or SEED
- use the file
- for each FPEAK or SEED
mypmft.ini
- as a template to create the file
imupmf.ini
- which is used as the control file for PMF.
- In v2.03, the convergence criteria for completing the PMF calculations can be set proportional to Q/Qexp by changing headers in the PMF_Execution...ipf. The default is to use the convergence criteria in mypmft.ini.
- which is used as the control file for PMF.
//Settings for PMF Iteration Convergence proportional to Qexp constant ITERATION_CHI2_PROP_QEXP = 0 constant FIRST_ITER_LEVEL_PROP_CONST = 2e-6 constant SECOND_ITER_LEVEL_PROP_CONST = 2e-6 constant THIRD_ITER_LEVEL_PROP_CONST = 1e-6
- In v2.06 and higher, within the advanced tab of the PMF_performCalc_panel, the user may change PMF convergence criteria.
- You can read more about convergence criteria and large datasets in the PMF Users Manual Part 1 (pg. 10) (see Other Resources).
- Delete the old PMF2.LOG file by running delete_log.bat
- Execute PMF by running run_PMF.bat.
- Wait for PMF to complete its run.
- Load PMF output (including log file and factors)
At the completion of the loops, the software calculates some statistics from the output and then creates a panel to select data for viewing.
Bootstrapping (added in v2.02)
The bootstrapping mode is developed after the method described in the EPA PMF v3.0 Users Manual Sect. 6.4 (see Other Resources). The bootstrapping method is used to estimate the uncertainty in both the factor mass spectra and time series. This is achieved by running PMF on the full dataset once (from one PMF solution (i.e., combination of number of factors and fpeak) at a time) and then making a series of variations (the number is specified by the user when selecting the bootstrapping mode) in which a subset of the original rows (mass spectra) are randomly replaced by other rows from the original matrix and running PMF on each of these.
For each new PMF case ("bootstrapped case"), the resultant factors are compared to those from the original dataset and assigned as "matching" the original factor with which it has the highest correlation. Bootstrapped cases in which each bootstrapped factor was matched to exactly one of the original factors (i.e., there is a one-to-one mapping between original factors and those from the individual boot-strapped cases) are retained for calculation of the average mass spectrum and time series of bootstrapped factors. Plots of the original factors and the average bootstrap factors with 1-sigma variation bars are produced automatically.
EPA PMF Users Manual recommends doing 100 bootstrap runs for final results.
A little more detail
All output from the bootstrapping runs is saved in folder root:pmf_bootstrap:.
Row (mass spectrum) replacement is performed by using the StatsResample function in Igor to select rows for replacement. The row values are then sorted in increasing order as a convenience.
- The 2d wave RowsToBeReplaced records the rows to be used in each bootstrapped case. Each column represents one bootstrap case. Each column lists the rows of the original matrix included in that bootstrapped case.
- The 2d wave ReplacementHistogram counts the number of times that each original matrix row was used in a bootstrap case. Each column represents one bootstrap case. Summing the rows of this matrix gives the total number of times that each original matrix row was was used in the bootstrapping cases.
The assignment of bootstrapped factors to the factors from the original case is made by Pearson R correlation. Factors are assigned only on the basis of mass spectral comparison, and each factor is assigned to one of the original factors.
- Note that this is different than in EPA PMF. Our code does not have a criterion for the lowest allowable correlation between bootstrapped and original factors. In EPA PMF, factors that fall below this limit are "unmapped"; no factors are "unmapped" in our code.
- Note that if the original case has factors that are very similar to each other, the assignment of the bootstrapped factors may be incorrect or ambiguous. No current work has been done to give guidance as to what "very similar" means. No sanity checks are made in the code for this type of situation.
- The 3d wave FactorProfile_Rval stores the correlation between the boostrapped and original factors. Rows represent the factors from the original case, columns represent the factors from the bootrapped cases, and layers represent each bootstrapped case.
- The 2d wave FactorProfileSort contains the number of the original factor to which each boostrapped factor (row) has been matched in the bootstrapped case (column). Columns which contain (e.g., in a case with three factors) "0, 1, 2" have factors which were uniquely matched to the columns in the original case; these will be included in the averages of mapped factors. Columns which contain duplicate entries (e.g., "0, 1, 0") have multiple factors that were matched to the same original factor; these cases will not be included in the averages of the mapped factors.
Note that the criteria for including bootstrapped cases in calculations of the average bootstrapped factors is different in our code than in EPA PMF. Bootstrapped cases in which two or more factors are mapped to the same original factor are not included in the averages in our code. In these instances, the whole bootstrapping case is rejected before calculating averages. In EPA PMF, all bootstrapped factors mapped to the same original factor are included in the average.
Important: At the present time (v. 2.02) the plots produced by the bootstrapping code expect to find the waves noNaNs_amus (for plotting profiles) and noNaNs_t_series (for plotting time series). If these are not the names of your waves that describe the columns and rows, respectively) of the input matrix, you should duplicate your row and column description waves to have these names.
Running Two Simultaneous Analyses on Dual-Processor Computers
You can run two PMF analyses (in two separate experiments) on the same computer simultaneously if you have dual processors. Each analysis will run at the same speed as on a single-processor computer (or when one analysis is run on the dual processor computer). The PMF executable is not "multi-processor aware," meaning that it can not utilize both processors simultaneously for one PMF run.
To run two simultaneous analyses with the PET, you'll need two directories on your computer with the PMF .exe, .key, and mypfmt.ini files. The directory names must end in "1" and "2," respectively. For example, you could have
- C:\PMF\PMF Executable1
- pmf2wtst.exe
- pmf2key.key
- mypmft.ini
- C:\PMF\PMF Executable2
- pmf2wtst.exe
- pmf2key.key
- mypmft.ini
Each experiment running PMF must use a separate Executable directory. While a PMF analysis associated with a PMF Executable directory is running, a file called "PMFrunning.txt" exists in that directory. If you try to run your second PMF analysis using the same Executable directory, the PET will give you an error. You can choose a different Executable directory and press the button to start the analysis.
Convergence
PMF uses a variety of metrics to assess the progress of finding a solution. Some of these metrics are based on parameters that were initially optimized for AMS data, and hence, may not be appropriate for other data sets. The last tab in the PMF_PerformCalcs panel has a section entitled Q convergence criteria which lists some defaults; users may modify these values to achieve convergence. The log text file, PMF2.LOG generates information about the progress for finding a solution. As an example the following is an excerpt that was written to this file:
The log text file, PMF2.LOG generates information about the progress for finding a solution. Below is an excerpt from a file where a PMF solution didn't converge.
299 rank1 step chi2= 6.22372E+06 Penalty= 2.5296E+04 Flags GF 300 rank1 step chi2= 6.22364E+06 Penalty= 2.5295E+04 Flags GF
************************************************************ 1 */ Iteration interrupted because maximum step count *\ has been exceeded in the robust mode. NO CONVERGENCE? ************************************************************ 1 300 iter-steps in all. Final chi2= 6223643.5000 in the robust mode.
As a practical matter, the last version of the PMF solution is saved within PET and users can view this last result for this PMF run. However, because it did not converge graphs in the main PMF panel will be grayed out and the Q/Qexp value will be blank.
View PMF Analysis Results *Step 2*
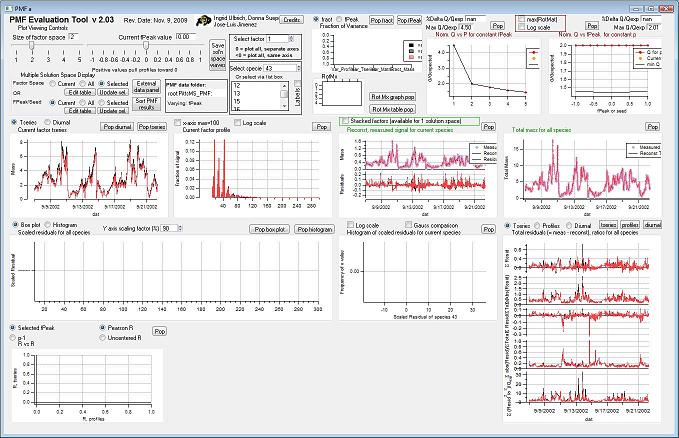
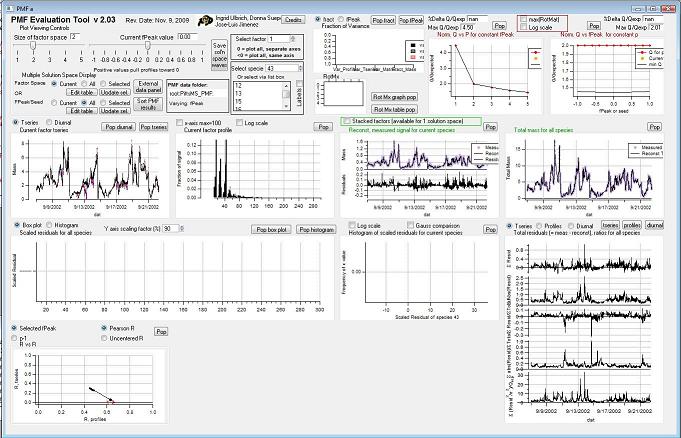
Controls
Factor Space and Fpeak Slider
Save Solution Space Waves
Select Factor
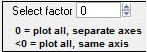
|
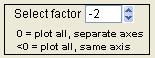
|
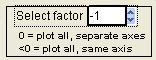
|
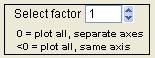
|
Select species
Select Multiple Factors or Fpeak/Seed
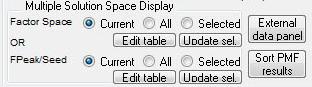
|
|
|
|
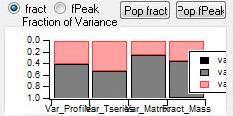
Mass Fraction
Mass Fraction/Variance
RotMx
Q Plots
Q versus Number of Factors
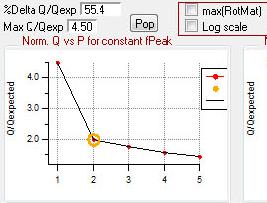
|
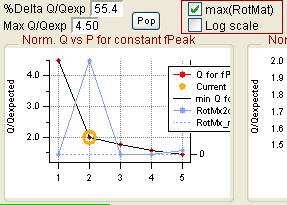
|
Q versus fpeak/seed
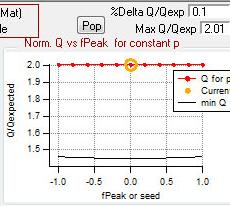
|
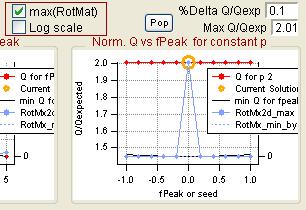
|
Factor Graphs
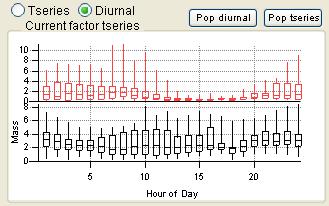
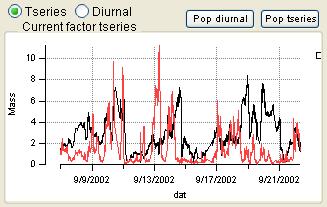
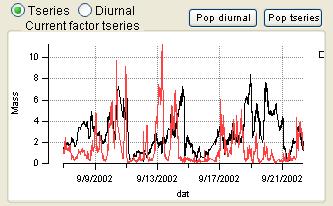
Time Series
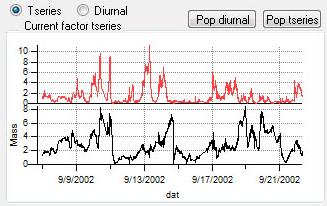
|
|
|
|
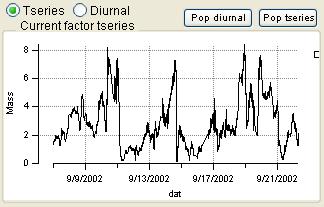
|
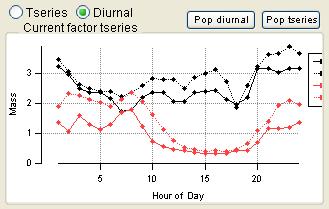
|
Profiles (usually Mass Spectra)
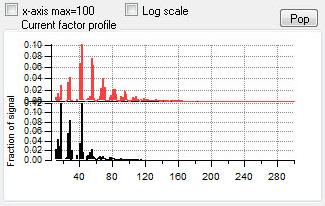
|
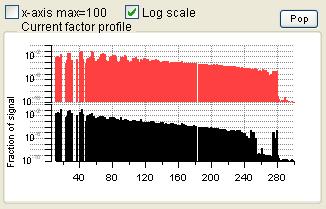
|
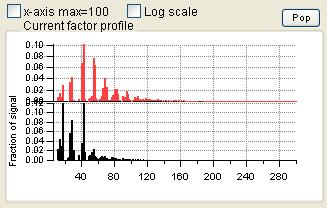
|
|
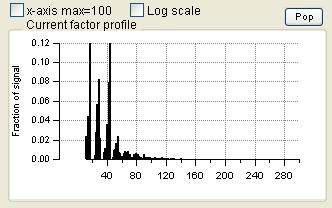
|
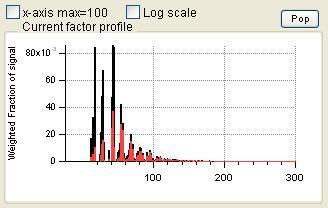
Reconstruction and Residuals
Total Reconstruction
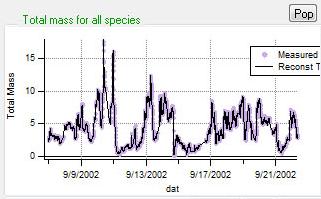
|

|
Total Residuals
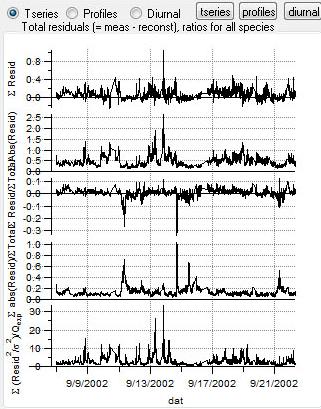
|
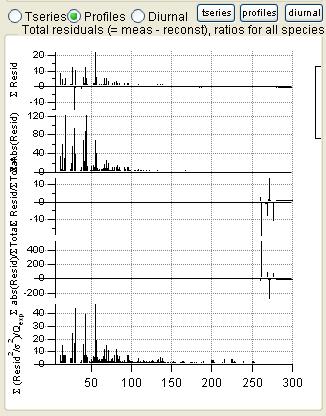
|
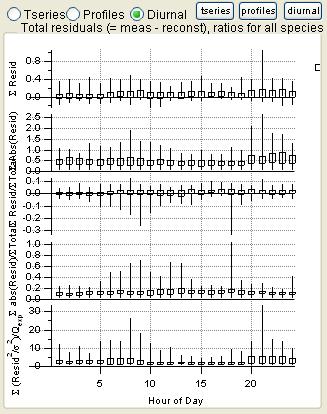
|
Current Species Reconstruction and Residual
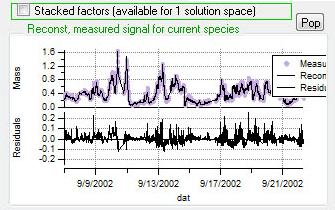
|
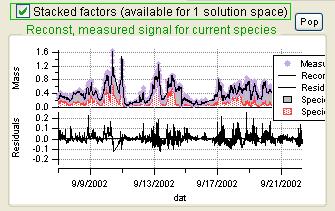
|
Scaled Residuals
All Species Scaled Residuals
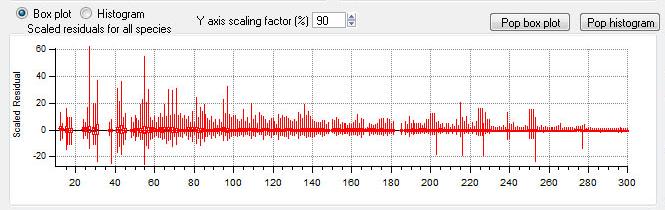
|
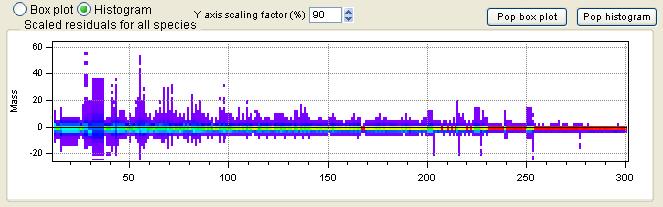
|
Current Species Scaled Residuals
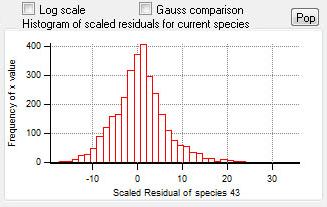
|
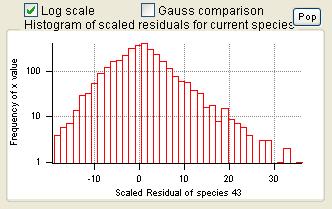
|
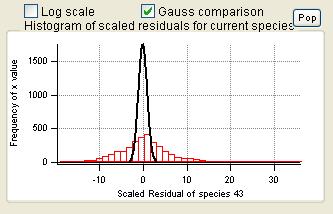
|
"RR" plot
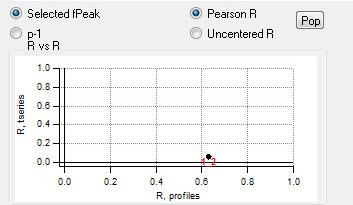
|
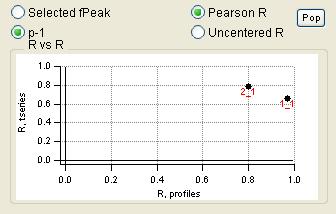
|
AMS loadings and the RIE, CE and CDCE factors
When exporting species like Org and HROrg from all versions of Squirrel and Pika, users should be aware that the RIE or the CE or CDCE factors are not applied to the 2-dimensional data. The reasons for this rule are somewhat historical. Basically, whenever a result in Squirrel or Pika retains an MS dimension, as in the export of the 2D wave for PMF, which has dimensions of measurement time and UMR or HR mass values, the RIE and CE (or CDCE or HR CDCE values) are not applied.
Users may wish to compare factors and loading from PMF results to species time series loadings with the RIE or CE applied. Below is a guide for applying default RIE and HR CDCE to source factors within a PET experiment; similar operations can be used for CE or UMR CDCE. Be aware that by performing this operation, the user assumes that the RIE and CE (or CDCE or HR CDCE) is the same for all factors. This may not reflect reality. For example RIE calibrations and CE (or CDCE or HR CDCE) have been generated for bulk ambient organic aerosol; the RIE and CE for BBOA and COA, for example, may not be identical.
There are 3 main steps to incorporating the RIE and CE (or CDCE or HR CDCE) to PMF factors.
1. Generate a 1D wave matching the time series wave containing a multiplicative factor of the RIE and CE or CDCE and import it to the PMF experiment.
2. Remove points in this 1D wave that matches the nans removed in the data prep step of PMF.
3. Divide this wave to your time series factor waves in the PMF experiment.
More details and example of commands are below.
Step 1. Within your Pika experiment, the HR CDCE is root:HRCE_fphase; for UMR data it is root:CE_fphase. The RIE values can be found in the UMR or HR batch tables. Here are commands you can use and modify as needed.
Duplicate/o root:HRCE_fphase root:HRRIECEfactor // Use a similar command for UMR. This wave should be the same length as the t_series wave
root:HRRIECEfactor *= 1.4 // 1.4 is the RIE of HROrg in this data. We will divide the PMF factors by this HRRIECEfactor wave.
Save/T/M="\r\n" HRRIECEfactor as "HRRIECEfactor.itx" // Save this wave as separate itx file.
In this example I saved this file in the same place as the exported PMF text file (that you had loaded into your PMR experiment at the beginning of that analysis). You can also load this wave into your PMF experiment via the browse experiment command without saving it as an external text file.
Step 2. There are a few ways to accomplish this step. Within your PMF experiment and data folder containing the original data (before noNan_* versions of the data was created, create a time series wave to flag when rows (time points) were nan.
Load the HRRIECEfactor wave from step 1 and multiply this wave by it.
LoadWave/T "HRRIECEfactor.itx"
MatrixOp/o HRtimeseries = sumRows(HROrg) // HRtimeseries will be n x 1 matrix with nans in the correct places.
HRtimeseries /=HRtimeseries // make all the values in this wave nans or 1s.
HRRIECEfactor*=HRtimeseries // nan the correct time points
RemoveNaNs(HRRIECEfactor) // The Remove Points ipf containing this RemoveNaNs function should automatically be loaded into the PMF experiment via the line #include <remove points> in the PET scatter ipf.
Step 3. In the main results PMF panel, current factor tseries graph, the y waves are named root:pmf_plot_globals:TSeriesFactor1, root:pmf_plot_globals:TSeriesFactor2, etc. for any factor solution. You may choose to simply copy and divide these waves directly (all assuming you are in the same data folder as in step 1):
duplicate/o root:pmf_plot_globals:TSeriesFactor1 TSeriesFactor1RIECDCE
duplicate/o root:pmf_plot_globals:TSeriesFactor2 TSeriesFactor2RIECDCE //...
TSeriesFactor1RIECDCE/=HRRIECEfactor
TSeriesFactor2RIECDCE/=HRRIECEfactor //...
Know that any time you reselect the factor solution (fpeak, number of factors) in the main results panel, you will need to redo this duplication and division.
AMS HR factors colored by families hack
Versions 3.0 and higher of PET have incorporated data and code to create elemental ratios for High resolution AMS data. Information below is only useful for older (2.x versions of PET.
As of PMF version 2.08D, the grouping of HR ions info CH, CHO1 etc families and elemental ratios of factors is built into thePMF "View Results" panel. For historical purposes, a 'hack' for performing these tasks for use with older PMF versions is described below.
During the examination of factors of High Resolution AMS spectra, it is often helpful to plot the HR spectra summed into chemical 'families', i.e. familyCH which consists of all chemical fragments consisting only of C and H atoms, in a unit resolution dimension. As of November 2013 the following method can be employed.
(1) Add the ipf named HR_PMFsupplemental_v1_1.ipf to your PMF experiment.
(2) From the pika experiment from which the HR spectra was generated, copy the entire folder named HR into the PMF experiment. This can easily be done via the Data Browser - Browse Experiment feature in Igor. Specifically, in your PMF experiment, press the Browse Experiment button, select the pika experiment, and then in the right hand side of the window click and drag the HR data folder over to the left hand side, so that the cursor points to the root folder. The PMF experiment should now have the waves root:HR:HR_family_B copied into it. Not all the waves in this folder will be used, but it is easiest to simply copy them all.
(3) Execute the following line, or analagous, to calculate and plot the HR family grouped spectrum for a currently chosen PMF factor of interest. BreakHRSpectraIntoUMRFamilies(root:pmf_plot_globals:profilefactor1, root:noNaNs_ExactMassWaveNoIso, root:noNaNs_ExactMassTextNoIso, 1)
In the line of code above, the first parameter indicates which currently displayed HR factor is to be calculated. The second and third parameters indicate the HR mass value and the Mass Text identifier waves of the HR spectrum. These waves should be exactly the same as those you chose in Step 2 of the PMF tool, Description of COLUMNS of Data matrix (numbers) and (text). The last parameter is a simple true/false flag for indicating whether or not to plot and color the results.
Subsequent executions of the line, i.e. BreakHRSpectraIntoUMRFamilies(root:pmf_plot_globals:profilefactor2, root:noNaNs_ExactMassWaveNoIso, root:noNaNs_ExactMassTextNoIso, 1) will generate a new HR colored spectrum for the second factor (of the currently selected PMF solution).
Compare PMF Results with External Factors *Step 3*
Caution: This part of the code is a bit fussy! Please contact Ingrid if you have tried the tips here and have trouble getting this panel to work.
Setting up the External Data
- Check that the waves NaNsWv_amus" and "NaNsWv_tseries" (these were created when you deleted NaNs from your original matrix) are in the datafolder where your PMF output is being saved. If they're not already there, you'll need to find them and copy them to this location.
- Versions 2.02 and lower used the strings "NaNsList_amus" and "NaNsList_t_series" to record the location of deleted NaNs. If you are upgrading experiments, make sure that these strings are in the folder where your PMF output is being saved; "NaNsWv_amus" and "NaNsWv_tseries" will be created and used for future calculations.
- You'll need separate folders (in root: ; they cannot be in a lower directory) for mass spectra and time series you want to use for comparison to the factors.
- The tricky part of using this panel is setting up your mass spectra and time series correctly.
- Each wave must have either the same number of points as in the corresponding dimension of your noNaNs_ data matrix or the same number of points as in the corresponding dimension of your original matrix.
- For example, if your original matrix is 3246 rows and 300 columns and your noNaNs_ matrix is 3200 rows and 268 columns, your "external" mass spectra can have 300 or 268 points; "external" time series can have 3246 or 3200 points.
- As another example, if your original matrix is 100 rows and 320 columns and your "external" mass spectra has 300 points then you may extend the external mass spectra to 320 points, inserting nan values in the last m/z 301 - m/z 320 rows.
- For mass spectral comparisons, download "full" spectra (usually 300 points) from the AMS Spectral Database instead of using the shortened ones provided in the 9th Users Meeting template. You should inspect the length of all waves from the Database to make sure that every one has the correct number of points for your work.
- Each wave must have either the same number of points as in the corresponding dimension of your noNaNs_ data matrix or the same number of points as in the corresponding dimension of your original matrix.
- IMPORTANT NOTES
- The reason for the restriction on the number of points in "external" comparison waves is the following: After you select the datafolders for the external mass spectra and time series, the code makes a folder inside each of these folders called "noNaNs". Each wave in the external datafolder is copied to the new directory. Then the code checks whether the waves have the same number of points as the same dimension in the matrix used to run PMF; if so, no change is made to the wave. If not, the code _assumes_ that the wave has the dimension of the original matrix (which it doesn't know about) and therefore uses the string "NaNsList_amus" or "NaNsList_t_series" to delete the rows that it believes were NaN in the original dataset. (It's ok if these waves still have NaNs (e.g., missing points in data from another instrument when the AMS data was good); only the points where both the factor and external waves have valid data are included in the correlation calculation.)
- Because of some internal coding restrictions, time series waves for comparison cannot include the string "series" in their name; such waves will not be created in the noNaNs folder.
- Each of the mass spectral and time series waves must be 1-dimensional. This means that you cannot use the waves from root:pmf_plot_globals: called TseriesFactor1, TseriesFactor2, etc. since these are 2-dimensional waves.
- Old versions of the mass spectra in the AMS Spectral Database have m/z = point number, meaning that point 0 = m/z 0. This is not usually the way that AMS matrices are saved from James' software or from Squirrel, so you may need to delete 1 point from the beginning of each spectrum that you use from the Database. This is important to check, or else you correlate the wrong m/z's with each other.
Choosing the Folders with External Data
- The first time you want to calculate factors you can do so by pressing the "External Data Panel" button on the main panel or by choosing from the PMF pulldown menu "Compare PMF results with External Factors *Step 3*".
- Note that after you have accessed the "External Data Locations" panel, pressing the "External Data Panel" button on the main panel will not bring you back to the selection panel again. To choose different folders or force recalculations you must access the selection panel from the PMF pulldown menu.
- Select your external data folders.
- Other choices from the pulldown menus include
- "No external data of this type": The PET will not attempt to calculate correlations between factors and external data of this type.
- "Update List": If after calculating factor correlations you wish to add new external waves of this type, choose this option to add the correlations for the new waves do your existing list of correlations.
- Other choices from the pulldown menus include
- Press the button to proceed.
What the PET Does (and how to fix things if something goes wrong)
- In each external data folder, a folder called "noNaNs" is created as described in the IMPORTANT Note 1 above (item 3 of Setting Up the External Data).
- Each of these new waves is compared to every factor wave. (This can take a while if you have a lot of waves for comparison.)
- If the factor and external waves have different lengths, the function aborts and tells you that the comparison function was called with waves of different lengths. Unfortunately, it doesn't give helpful information about which wave had the wrong length (we'll try to look into that and improve that error message).
- If this happens, you should look in the "noNaNs" folder in the appropriate external data folder and check whether all of the waves have the correct length. Waves with incorrect numbers of points in this folder may be the result of incorrect wave lengths in the "external data" folder. Try to fix all of the problem waves and then run the function for calculating the scatter comparison again by choosing step 3 from the PMF pull-down menu. Recall that this is the only way to force recalculation of the comparison of the factors!
- If forcing recalculation didn't fix the problem, delete the "noNaNs" folder in the appropriate external data folder and then recalculate again.
- If this happens, you should look in the "noNaNs" folder in the appropriate external data folder and check whether all of the waves have the correct length. Waves with incorrect numbers of points in this folder may be the result of incorrect wave lengths in the "external data" folder. Try to fix all of the problem waves and then run the function for calculating the scatter comparison again by choosing step 3 from the PMF pull-down menu. Recall that this is the only way to force recalculation of the comparison of the factors!
- If the factor and external waves have different lengths, the function aborts and tells you that the comparison function was called with waves of different lengths. Unfortunately, it doesn't give helpful information about which wave had the wrong length (we'll try to look into that and improve that error message).
- The correlation values between the factor waves and the external data waves are stored in waves in the folder with PMF output called
- "RcorrMx4d_Profiles" and "RcorrMx4d_Tseries" (with Pearson R)
- "RcorrMx4d_Profiles_pear_mzGrt44" (with Pearson R, only for m/z > 44)
- It is also possible use the function scat_calc_RCorrMx4d_UC() to calculate
- "RcorrMx4d_Profiles_UC" and "RcorrMx4d_Tseries_UC" (with the Uncentered Correlation, as reported in [ Ulbrich et al., ACP, 2009]
- When the calculation is complete, the Scatter Panel is created.
Other Potential Problems and Solutions
- Pulldown menus don't have lists. Each "noNaNs" folder should also contain a text wave called "TseriesWvsNms" for time series or "FactorWvsNms" for profiles. This wave is used for the pulldown menus in the panel. If this wave is missing, the pulldown menus may not work. There should also be a string of wave names in the folder called "TseriesWvsNmsList" or "FactorWvsNmsList"; if so, you can create the text wave by gen_list2txtWv(listStr, wvNm).
Some Other Notes
- Order of the factors. Factors are numbered 1 to N and match the factors in the main panel, counting from the bottom of the factor plots.
- Colors. Factor 1 is black, Factor 2 is red, Factor 3 is green, Factor 4 is blue, etc. Factors in this panel have the same color as they did in the main panel. In the overlay plots, the factor is its usual color and the external species is orange.
- Size of Factor Space and Current Fpeak value sliders. The sliders in this panel and in the main panel control both panels simultaneously. Graph updates are slower with both panels. Be patient and don't click on anything until everything has updated.
More Features
- Assign Groups to External Data. This feature allows you to reorder the external data waves and assign them to groups. Groups then define the colors used in the R bar plots in the panel and in the Comprehensive External Data Correlation Plot (below).
- Comprehensive External Data Correlation Plot. This plot display the "R vs External Factor" plots for all factors at once.
Considerations for Choosing a Solution
PMF Evaluation Tool Software
| Version | Date | Release Notes | PET ipf files | PET Template | mypmft.ini | ||
|---|---|---|---|---|---|---|---|
| 3.08D | 12 Dec 2023 | Release Notes v3.00 | Zipped PMF file containing these 7 ipfs:
PMF_SetupPanel_v3_08D.ipf |
or | Igor PMF template experiment v3_08D | and | mypmft.ini for use with v2.03 and higher |
Quick review: Igor code called PET (PMF evaluation tool) assists in a PMF analysis. Anyone with credentials can download PET; there is no need to request an individual account. When you click on a link to download, a prompt should appear asking for credentials. If you need credentials email Donna The PET code v3.08 has been tested on these versions of Igor: 6.37, 7.08, 8.04, 9.0.2
PMF executable code is required for PET to interface with. PMF is available for purchase from Penti Paatero, Paatero and you must email and pay him separately and after payment he will provide a license key which allows PMF to run. The Igor PET code is not needed to run PMF; PET provides a handy interface to generate and view PMF results.
BareBones Starter Kit
Download the BareBones_PMF_Starter_Kit.zip described for initial installation of PMF on a computer.
Bug in code previous to version 2.08 (spring 2017)
The details: the bug is in step 6 of the Prep tab of the PMF_PerformCalc_panel in PET. This bug occurs when the user presses the "Downweight weak, bad m/zs" button and chooses to 'Remove' 'bad' variables (default setting) and 'bad' variables exist. The bug is serious in that during this step some columns in the data matrix *may have been overwritten*. When this happens PMF results could have been degraded. Yet it is very unlikely that any scientific conclusions will be upended.
Regarding the PET + Igor versions when this happened: - In PET versions previous to 2.05 (2012) and earlier it is unclear how users handled 'bad' variables. It is conceivable that if PET users incorporated a proto-type of later code that handled 'bad' variables then this bug would exist. At least by December, 2012, PET 2.06Beta, the bug existed. - In Igor 6.x and PET versions 2.05 up to version 3, this bug will not generate an obvious error (even though this bug/error occurred!). - If you are using Igor 7 OR are using PET versions 2.08-2.09Z or higher, you will get a Wavemetrics generated 'out-of-index' error and the code will stop executing. You would not be able to continue.
The bug is that the code will incorrectly overwrite the right-most columns of the data matrix (corresponding to the highest m/z if the matrix columns are in increasing m/z order (default for AMS Org, HROrg, etc). The number of right-most columns that are incorrectly overwritten is dependent on the SNR (signal to noise ratio) and the column location of 'bad' variables. The more 'bad' variables were flagged, the larger the number of columns that were incorrectly overwritten. The behavior is an 'out-of-index' error; in Igor 6 or PET versions < 3.00 the overwritten (right-most) columns begin to become (incorrectly) identical. If you do not have 'bad' variables or have chosen to downweight instead of remove them, the data matrix is correct and your analysis will not be affected.
Because the right-most columns generally correspond to signal with relatively little variability, the net effect on PMF results is likely minimal. If you combined any other signal (i.e. inorganic) by appending columns to the right of the main organic matrix, it is likely these right-most (i.e. inorganic) signals are compromised.
Note that it is only the data matrix that is potentially compromised. The error matrix was 'correctly' generated. However, if the data matrix is compromised, then the problem is that the right-most, last (bad) columns are paired with semi-random errors and PMF is trying to make sense of it.
Who should check their PMF results? - Anyone who analyzed data in Igor 6.x or using PET's code, versions before 2.08, and performed the automatic removal of bad variables. - If you used PET 2.08+ OR used Igor 7+ to perform the error preparation steps, you are fine.
How can you tell if your previously analyzed PMF results were compromised? Several methods are available: (A) In the history window search for the words "bad/weak columns" For example // Removed 3 bad/weak columns. in the history window indicates that in step 6, 3 columns were removed. In this case, the right-most 3 columns in the data matrix are possibly incorrect. The impact of your results could be proportional to the number of columns removed divided by the total number of columns, or probably less than that, if those are high m/z with low SNR.
OR
(B) In the main PMF evaluation panel, select the largest species (for HR ions) or largest UMR m/z that was analyzed. Notice the time series graph of this species (or m/z) titled "Reconst., measured signal for current species", and the top-most, purple trace. Now select the second largest specie or m/z. Did the purple trace change? If it did not change, this is an indication that the data matrix is compromised.
OR
(C) Make a table of the no-nans data matrix, the one used as input to the PMF (selected in PET tab “Run”). Scroll to the right-most columns and see if columns begin to be identical. If so, the data matrix is compromised.
What should I do if my PMF results were affected?
It is likely that your scientific conclusions are OKnot faulty. But the best thing to do is to redo the PMF analysis with PET version 2.08 or higher or in Igor 7. In PET, the first tab, you can use the yellow "Clear error prep work' button and start over without having to reload in the original data and error matricies.
PET version 3.0 has been uploaded to the web site and fixes the bug.
Other Resources
To order the PMF software email Paatero
- Ingrid's presentation of the PET at the 9th AMS Users Meeting in three parts (1. Overview and PMF Execution; 2. Viewing PMF Results; 3. Using the Scatter Plot Panel)
- The tutorial data used with that presentation
- Manjula's overview presentation of PMF at the 21st AMS Users Meeting (virtual, 2021)
- Donna's presentation of extending AMS data sets beyond Org or HROrg at 21st AMS Users Meeting (virtual, 2021)
Some PMF Method Papers
- Paatero, P., and Tapper, U.: Analysis of different modes of factor analysis as least squares fit problems, Chemom. Intell. Lab. Syst., 18, 183-194, 1993. Abstract
- Paatero, P., and Tapper, U.: Positive Matrix Factorization: a non-negative factor model with optimal utilization of error estimates of data values, Environmetrics, 5, 111-126, 1994. Abstract
- Paatero, P.: Least squares formulation of robust non-negative factor analysis, Chemom. Intell. Lab. Syst., 37, 23-35, 1997. Abstract
- Paatero, P., Hopke, P. K., Song, X. H., and Ramadan, Z.: Understanding and controlling rotations in factor analytic models, Chemom. Intell. Lab. Syst., 60, 253-264, 2002. Abstract
- Paatero, P., and Hopke, P. K.: Discarding or downweighting high-noise variables in factor analytic models, Anal. Chim. Acta, 490, 277-289, 10.1016/s0003-2670(02)01643-4, 2003. Abstract
- Paatero, P., Hopke, P. K., Begum, B. A., and Biswas, S. K.: A graphical diagnostic method for assessing the rotation in factor analytical models of atmospheric pollution, Atmos. Environ., 39, 193-201, 10.1016/j.atmosenv.2004.08.018, 2005. Abstract
- Paatero, P., and Hopke, P. K.: Rotational Tools for Factor Analytic Models, J. Chemom., 23, 91-100, 10.1002/cem.1197, 2009. Abstract