| Intro | Seismology | Heat flow | Gravity | Conclusions | References |
| Low velocity zone | Traditional techniques | ||||
| Mantle stratification (via receiver functions) | Admittance | ||||
| Coherence |
Gravity: Spectral Techniques
Spectral gravity techniques examine the relationship between gravity anomalies and topography in the wavenumber domain. The basic idea is to examine how the lithosphere responds to topographic loads of different wavelengths. For example, building a skyscraper will not cause a depression of the Moho; instead, the load will be flexurally compensated. How large a “skyscraper” or mountain belt can be accommodated by flexure of the lithosphere with the necessity of Airy or Pratt isostatic compensation is a function of the strength of the lithosphere (i.e. its flexural rigidity, D, or elastic thickness, Te).
This elastic thickness can be viewed as a proxy for lithospheric thickness. It is argued [Artemieva, 2006] that Te represents the depth to the 550 C isotherm in lithosphere older than ~200 Ma, citing a critical decrease in strength of olivine above this temperature. As a side note, younger, feldspathic lithosphere may have critical temperature of ~350 C. Thus in a one-dimensional conductive regime, there will be a linear relationship between elastic and overall lithospheric thickness.
In the following discussion it will be useful to bear a few equations in mind.
Wavenumber: k = 2π/λ where λ is the wavelength
Elastic thickness: Te=12(1-ν2)D/E where v=Poisson’s ratio; E=Young’s Modulus
Admittance
Admittance is the set of coefficients (as a function of wavenumber or wavelength of the topographic load) to scale topography, H(k) to gravity anomaly, Δg(k).
Admittance: Z(k)=Δg(k)/Η(k)
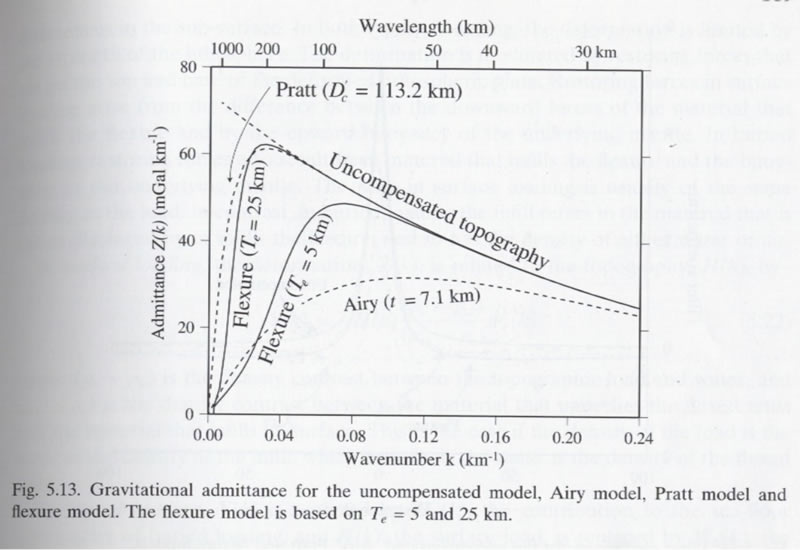
Unfortunately, Z(k) will depend on the isostatic or flexural model chosen (see figure below, from Watts, 2001), so it requires certain assumptions about the state of loads on, in, and at the base of the lithosphere [Forsyth, 1985].

For example, a solution for the free air admittance of surface loading that is flexurally compensated:
Z(k)=Δg(k)/Η(k)
Δg(k)=2πGρce-kε(1-Φ(k) e-kt) H(k)
Z(k)=2πGρce-kε(1-Φ(k) e-kt)
where ε is the elevation of the observation (i.e. the surface elevation or the altitude of an airborne observation)
and where t is the mean crustal thickness
and where Φ(k)=[ Dk4/(rm-rc)g +1 ] -1 .
Note that information on D, the flexural rigidity, is hidden in the scaling of topographic signals to gravity signals but is also obscured by assumptions regarding crustal thickness and crust and mantle densities.