FAQ for AMS Data Users
- The purpose of this page is to serve as a repository of answers to frequently asked questions from users of AMS data products, much of it for general AMS applications, but some of it specific to the CU aircraft AMS.
- Contributions are most welcome, and should be directed to the curator of the page (JL Jimenez as of Dec. 2016).
- A shorcut to this page is http://tinyurl.com/FAQ-AMS-Data
- This page should be cited as "J.L. Jimenez, P. Campuzano-Jost, D.A. Day, B.A. Nault, H. Guo, J.C. Schroder, M.J. Cubison, Frequently AMS Questions for AMS Data Users, http://cires1.colorado.edu/jimenez-group/wiki/index.php/FAQ_for_AMS_Data_Users, accessed month-year"
General AMS FAQs
Which species and size range does the AMS measure and not measure?
- The AMS measures submicron aerosols. The details of the transmission curve of the AMS are discussed at this link below.
- A new aerodynamic lens is being developed which allows measurements of supermicron aerosols as well, see Xu et al., AS&T 2016 and Peck et al., AS&T 2016. As of Dec 2016 this is still a prototype system and very few AMSs are using it.
- The AMS measures non-refractory species, which are those that evaporate in a second or less at 600C under high vacuum. In practice this includes the secondary inorganic salts (ammonium sulfate, ammonium nitrate, ammonium chloride) and organic species.
- The AMS has traditionally been assumed to not measure dust and metals, sea salt, and black carbon. However recent research has shown some capabilities in this regard.
- The use of the background signal allows the detection of slowly-evaporating species on timescales of several hours instead of 1 s. This allows detecting species with vapor pressures ~4 orders of magnitude lower than traditional non-refractory species. We refer to those as "semi-refractory" species. See Salcedo et al. (ACP 2011) for a description of the method and its application to Pb measurements. As of May 2016 this analysis requires custom analysis which is not part of the standard AMS software.
- Ovadnevaite et al. (JGR 2012) demonstrated the detection of submicron sea salt with the AMS. This requires sampling humid aerosols (i.e. w/o a dryer). There is some debate about this capability in the literature.
- A new version of the AMS (Soot-Particle AMS, SP-AMS, Onasch et al., AS&T 2012) allows the detection of black-carbon by using laser-induced incandescence vaporization, instead of the traditional tungsten vaporizer.
Are particles dry or wet when sampled in the AMS?
- Particles lose water in the aerodynamic lens, thus we typically do not report concentrations of particle-phase water (see next FAQ).
- On aircraft the airflow into the AMS is typically not dried, but RH is typically low because of the heating from ram and heat transfer in the cabin. An estimate of the actual humidity just before the AMS can be derived by assuming that the absolute humidity (% or ppm of H2O) is the same as in the air outside of the plane. Then the inside RH can be calculated from the absolute humidity (calculated from the outside RH and temperature) and the measured temperature of the AMS inlet in the cabin. Depending on aircraft speed and altitude the heating can vary between ~15C-50C. Since an increase of 1C corresponds to a decrease of ~5% RH, humidities in the AMS inlet are typically low.
- On ground-based studies using the standard vaporizer it is highly recommended to dry the particles using a steel-encased nafion dryer to reduce variations in collection efficiency arising from particles that retain significant water in the AMS (e.g. Allan et al., JGR 2004). However not all AMS users follow this procedure.
- Detection of submicron sea salt does not work if the particles are dried, and some users in marine studies do not dry for this reason.
- The new capture vaporizer (CV) has a collection efficiency around 100%, and it is expected that drying will no longer be necessary when using it. As of May 2016 studies comparing dried vs. not dried aerosol with the CV have not been reported, to our knowledge.
Can the AMS measure particle-phase water?
- Most aerosol water is lost in the aerodynamic lens (e.g. Zelenyuk et al., 2006). However under some conditions (such as high RH or acidic particles with ammonium deficit) some water can be retained and detected with the AMS (Matthew et al., 2009; Englehart et al., 2012). Quantifying this particle-phase water is difficult because the thermal decomposition of sulfates and OA also produces H2O(g) in the AMS vaporizer, and gas-phase water also produces a signal. Those three additional sources of water are often as large as the remaining particle-phase water, and they are difficult to quantify. For this reason particle-phase water is very rarely reported for AMS datasets. However Englehart et al., 2012 did report particle water concentrations that agreed with an independent measurement. A possible explanation was that the loss of a relatively constant fraction of the particle water in the AMS lens (since composition was constant during that study), combined with the high relative ionization efficiency (RIE) of water. No followup study has attempted such a measurement to our knowledge.
- In addition, most ambient studies use a dryer (in order to be able to use the composition-dependent CE parameterization of Middlebrook et al. (2012)) and thus very little or no particle-phase water remains as the particles enter the AMS.
Should instrument response time be taken into account in intercomparisons?
- In aircraft comparisons with instruments that have a longer tail in response time (such as those based on ion-chromatography), the AMS data may need to be degraded with a one-sided function empirically-determined from the analysis of the response of both instruments to rapid and large changes in concentration. See pages 4-6 in this AMS Users Presentation by Cubison and Jimenez for further details.
Is there a glossary of AMS jargon I don't understand?
- Yes! The AMS is a complex instrument, and as a result we have created a large set of AMS-specific words and acronyms. This glossary is a work in progress, so please edit and/or send us questions on it!
Concentration FAQs
Are AMS concentrations always reported under STP or ambient conditions?
- This depends on the particular study and group. All papers reporting μg m-3 of aerosol should state the basis of the m-3 in the experimental section. Unfortunately this is not always the case, and the generators of the data should then be contacted.
- Note that sometimes an AMS User may not pay attention to this detail, so that the group generating the data doesn't even know how they are reporting. In that case it boils down to what the flowmeter used to calibrate the AMS flow reports, which can be either standard (with more than one definition, see below) or ambient at the location where the calibration was performed (which often is not the same location as where the measurements were performed).
- To avoid confusion, we recommend the use of the unit μg sm-3 or μg m-3(STP) (see below) for concentrations reported under STP conditions, and of μg m-3 or μg am-3 for concentrations reported under ambient conditions.
What are μg sm-3?
- μg sm-3 are μg m-3 converted to standard pressure and temperature (STP) conditions of 1013 mbar, 273K without any evaporation/condensation. These units are very useful when comparing data taken over a range of pressure and temperatures, such as aircraft data. They are also very useful when comparing aircraft data to data from ground sites, or data from different ground sites which have different ambient pressures and/or temperatures. Some people prefer to write “μg m-3 (STP)” instead of μg sm-3.
- Ratios to gas-phase species (e.g. OOA/Ox) are constant when expressed in μg sm-3 ppb-1, but not if μg m-3 are used.
- Note that unfortunately there are many other definitions of STP, many of which are compiled in this Wikipedia article. Some of them are also used in the aerosol field, so be aware of these possible differences, which can be of the order of 10%.
Inorganics FAQs
Are the AMS concentrations of sulfate (nitrate) reported as μg SO4 m-3, or μg S m-3 (or NO3 vs N)?
- The AMS measures the concentrations of SO4 (not only S), NO3 (not only N). For SO4 and NO3 the conversion is straightforward.
Why do you write SO4 & NO3 and not SO42- & NO3-?
- In the aerosol community people often don't add the charges because it is understood that those symbols refer to aerosol nitrate and sulfate.
- For the AMS, we also detect some signal as part of the SO4 & NO3 "species" which may arise from organonitrates and organosulfates, which are not ions (see e.g. Farmer et al., PNAS 2010), thus it may not always be proper to use the charges. For example in this study by Fry et al. (ACP 2013) the NO3 detected by the AMS was almost completely organic.
- To prevent confusion between radical NO3 and particle NO3, which includes both organic and inorganic species, particle NO3 should be written as pNO3. For example, in this study by Nault et al. (ACPD 2018), total particle NO3 detected by the AMS was written as pNO3.
Are there losses of NH4NO3 in inlets during lab or ambient sampling?
- As summarized by Canagaratna et al. 2007, we generally do not see a size-dependence of nitrate calibrations, that would be expected if there was significant evaporation in the lab.
- Evaporation in field studies is also thought to be negligible, for short residence times of a few s. See this FAQ below for details. For longer sampling times (e.g. minutes) there can be significant evaporation, and we are preparing a paper on this topic.
What chloride does the AMS measure?
- All AMSs report non-refractory chloride, which is typically NH4Cl. Chloride in organic molecules could also be detected this way, but this has not been important in past studies to our knowledge. NaCl evaporates too slowly in the regular AMS "difference mode" and is not included in the non-refractory chloride.
- A separate method has been developed to measure NaCl with the AMS by Ovadnevaite et al. (2012), and verified more recently by our group and others. If this chloride is reported, it is separate (in addition to) the non-refractory chloride.
Organic Aerosol (OA) FAQs
Is the AMS OA the same as "OC" or "organic carbon" measured with other instruments and reported by some models?
- The AMS measures the organic aerosol mass (OA, sometimes also referred to as OM in older literature) and not only the OC or C. Sometimes modelers use the term OC when they really mean OA, this is very confusing and should be avoided. The term OA is nearly standard in the field now (e.g. see this large review of global models of OA by Tsigaridis et al. (ACP 2014)). To convert between OA and OC one needs the OA/OC ratio (also known as OM/OC ratio in older literature), which is measured by the HR-AMS and can also be quantified by other methods.
- OA correspond to organic aerosol mass (sometimes referred to as OM in older literature). It includes OC (organic carbon), as well other atoms (H,O,N) in organic species. See Aiken et al. (Environ. Sci. Technol. 2008) and Canagaratna et al. (ACP 2015) for details.
- The term "organics" is used in the AMS analysis software, but should be avoided in presentations and publications as it causes confusion with gas-phase organics.
How come you report both OA and OC in some datasets?
- The high resolution AMS can measure the OA/OC which is needed for this conversion (OC = OA / (OA/OC) ), as described in the previous question. Thus in some cases we report both OA and OC.
What units are elemental ratios reported in?
- Elemental ratios (e.g., oxygen-to-carbon (O/C), hydrogen-to-carbon (H/C), N/C, S/C) are always reported as MOLAR (i.e. atomic) ratios. On the other hand, OA/OC (or in older literature, OM/OC) is always reported as a mass ratio (since molar quantities of OA cannot be determined by AMS or most methods used to measure this ratio). Sometimes the carbon oxidation state (OSc, dimensionless) is calculated for AMS OA and is generally approximated as 2 O/C – H/C (using the molar quantities, see Kroll et al., 2011).
Can the Unit Resolution (UMR) AMS and ACSM report OA elemental ratios?
- It is not possible to do N or S with the non-HR AMS. Even with the HR AMS it is difficult, as they are typically quite small in ambient data, and one needs high signal and the higher resolution modes (W mode or LToF) etc. In our group we have rarely reported N/C or S/C for this reason.
- For CHO, to do it more accurately one needs HR. There are some estimation procedures that have been derived for unit resolution (UMR) data by comparing the results for the same datasets when analyzed in UMR and HR (e.g. Aiken et al ES&T 2008 and Canagaratna et al. ACP 2015). But that's not as accurate, and has only been done for ambient OA. For unusual types of lab OA, it could be totally off.
Are there losses of OA to evaporation during sampling?
- While most aerosol water (but not all at high RH) can be lost in the aerodynamic lens (e.g. Zelenyuk et al., 2006; Matthew et al., 2009; Englehart et al., 2012), any species that are partitioned to the aerosol due to volatility will typically have vapor pressures at least 5 orders of magnitude lower (< 1e-5 mbar for semivolatile species, vs > 1 mbar for water). Evaporation rate is proportional to vapor pressure, and since water evaporates at a rate of ~1e4 monolayers s-1, semivolatile species can be estimated to evaporate at a rate of 0.1 monolayers s-1. This corresponds to 0.001 monolayers in the 10 ms residence time in the AMS aerodynamic lens. This is consistent with the widely-observed lack of evaporation of ammonium nitrate, a semivolatile species, in the AMS lens (Canagaratna et al., 2007).
- If the inlet and AMS are much warmer than ambient air, heating can increase vapor pressure and (given enough time) lead to substantial evaporation of aerosol species. The key strategies to avoid or limit such evaporation is to reduce the residence time under the hotter conditions as much as possible, and to dry the aerosol as late as possible before the AMS. Guo et al. (2016) evaluated whether volatilization biases associated with measurements of ammonium nitrate (a water soluble and highly semivolatile species) were present under aircraft operation during the WINTER campaign (when the air sampled was 15-40C colder than the instrumentation in the cabin of the aircraft, and sampling times were ~1 s). Guo et al. 2017 performed a similar analysis for the 2010 CalNex-LA campaign (~2 s residence time in AMS inlet, heating of ~10 C at night). NO3 concentrations, as measured by a PILS and an AMS as well as thermodynamic partitioning calculations, indicate volatilization biases were not present - in the AMS aerodynamic lens as well. Most ambient OA species have low volatility (e.g. Cappa and Jimenez, 2010). For OA species that are comparable to NO3 (semivolatile, soluble in water, and with high molecular diffusivity) we would not expect issues in similar measurements for the reasons described above. (Of course under specific measurement conditions in some studies, e.g. with longer inlet residence times, it is possible that evaporation could become significant).
- A related issue is the possibility that water-soluble species would evaporate from the aerosol after drying. El-Sayed et al. (2016) have reported a loss of WSOC after drying. Those authors used a post-drying residence time of 7 s, which is much longer than those typically used post-drying for the AMS (e.g. ~1 s in SOAS, ~0.5 s in WINTER, ~2 s in CalNex-LA) and the time in the aerodynamic lens (~0.01 s). Per the Guo et al. studies cited above, it appears unlikely that water-soluble OA species could evaporate under such short residence times. While this topic should be subject to additional research, it is unlikely that AMS data with very short post-drying residence times has significant biases due to this effect.
Does the AMS report organic nitrates?
- The nitrate reported by the AMS is the sum of inorganic and organic nitrates, and the fraction of both types of nitrates depends strongly on location and time. The concentration of organic nitrates can be estimated from the ratio of the NO2+/NO+ ions in the AMS as described by e.g. Fry et al. (ACP 2013). In some cases the presence of sea salt and mineral nitrates, or of nitrites, may interfere with the organic nitrate estimation procedure. As of Dec 2016 this is an area of research, and it is the AMS Users' responsibility to use additional information from their experiments to support their results, as well as stating the resulting uncertainties accurately. A summary of the results published to date for US and European sites using this method is in Ng et al. 2017.
Can the AMS measure the N/C of ambient organic aerosol?
- This can only be done with the W-mode of the HR-ToF-AMS or with the LToF-AMS, as the other instruments / modes do not have enough resolution to separate these ions, and their signals are low for ambient aerosols (see Aiken et al. ES&T 2008)). Even with W-mode data, this is quite difficult to do and requires very good instrument tuning and utmost care in the high-resolution fitting and data analysis. An analysis may produce good O/C and H/C ratios but bad N/C ratios, as O and H are much more abundant and not sensitive to fitting errors to the same degree as N-containing fragments are.
- For lab or chamber experiments, fog water, etc. in which the N/C is much higher than for ambient aerosols, this problem may not be as important.
- The N/C measured by the standard elemental analysis procedure needs to be supplemented by the N present as organonitrates, as described e.g. in Fry et al. (ACP 2013). If organic nitrates are not estimated directly, this would lead to an underestimation on the bulk N/C of OA. E.g. Docherty et al., ACP 2011 estimate that the N/C of OA in Riverside, California was underestimated by a factor of 2, due to the presence of organic nitrates.
Can the AMS measure the S/C of ambient organic aerosol?
- The AMS does detect some organic ions that contain S and thus an S/C atomic ratio can be calculated. This is thought to be accurate for species with C-S bonds like sulfonic acids, but to be a large underestimate for organosulfates (C-O-S bonding) due to the decomposition of those species into fragments that are normally lumped into the "sulfate" AMS species (see Farmer et al., PNAS, 2010). Docherty et al., ACP 2011 estimate that the S/C of OA in Riverside, California was underestimated by a factor of 25, due to the presence of organosulfates.
Detection Limits, Accuracy, and Precision FAQs
Is it normal that there are some negative concentrations?
- YES, THIS IS NORMAL. Any instrument has a certain amount of noise. In particular for instrument in which the measurements is determined as a signal minus a background (like AMS or CIMS), when measuring a zero concentration, equal numbers of positive and negative measurements should cancel out to provide an average of zero. When the concentrations are near detection limit, a significant fraction of the measurements may be negative. This fraction should be 50% in filtered air or extremely clean air, otherwise the instrument is not working properly. It is very important to NOT REMOVE the negative measurements from the analysis, as this would bias the averages. This is very important for datasets under very clean conditions, such as the ATom campaign.
- So in summary, a concentration cannot be negative. But a measurement of a concentration CAN be negative under low concentration conditions. There is nothing unphysical about it, it follows directly from the physics and mathematics of the instrument detection.
- Unfortunately this has proven confusing for many people, especially with some modelers and with experimenters familiar with chromatographic techniques where the convention is to report small numbers as "below detection limit." However that practice can result in a bias, and the quantification of averages at low concentrations is better if the negative numbers are kept.
How should I treat the values under detection limit?
- See previous question. You should always average them in. We carefully check that the periods in which we sample through a filter average to zero (see next question). So if you did something else than just use the reported numbers (e.g. discard negatives only, replace points by 1/2 * DL, discard values below DL etc.) you would be CREATING A BIAS on the dataset. Also note that points that are below DL at the reported resolution (e.g. 1 s or 1 min.) may be above DL after averaging to longer time periods such as 1 h, since DL scales as 1/sqrt(avg. time).
How are the detection limits estimated?
- Detection limits (DL) are typically estimated from measurements with the normal AMS modes while sampling through a total particle filter. Typical detection limits are given in Table 2 of DeCarlo et al. (Anal. Chem. 2006).
- Note that detection limits scale with the inverse of the square root of the averaging time. So if e.g. 10 min detection limits are provided, but you are interested in the 2 hr detection limits, those will be sqrt(10/120) ~ 0.29 x the 10-min detection limits.
- Drewnick et al. (AMT 2009) demonstrated a continuous method of estimating DLs from the variability in the background signals for different species. This is particularly useful where the time-series data has been collected before the instrument has had chance to reach equilibrium in terms of both chamber background and electronic stability. Typically these influences are most prevalent in airborne data, where the AMS is typically only spun-up a few hours before take-off. In addition, the influence of background ions is shown by Drewnick et al. to increase significantly when sampling large mass concentrations, and it according takes some time for these concentrations, and the associated rises in DLs, to fall back to their previous levels.
Do the detection limits change with the averaging time?
- Yes, detection limits change a lot with the averaging time used, and they are not meaningful unless the averaging time is also reported. From previous results, the DLs scale as the inverse sqrt of the averaging time.
- Continuous DL estimates can be derived with the method of Drewnick et al. (AMT 2009).
What are the accuracy and precision of AMS concentration measurements?
- The overall accuracy of an AMS mass concentration measurement for a given species is a convolution of many different uncertainties. However, many of these are statistically-independent and thus, when added in quadrature the larger errors dominate the overall uncertainty. A useful discussion summarizing the principal sources of uncertainty is given in the supplementary information for Bahreini et al., JGR, 2009. The authors estimated mass concentration accuracies (2-sigma) of 38% for OA and 34% for inorganic species. For ground based studies the accuracy may be better.
- Some AMS practitioners report accuracies of sometimes 5% or 10%. Except for specific laboratory studies where more factors may be tightly controlled or determined, those uncertainties are unrealistically small.
- Without the use of the capture vaporizer (CV) and/or a light-scattering module, the AMS mass accuracy is generally dominated by uncertainity in the particle collection efficiency due to particle bounce (Eb, see Huffman et al. AS&T 2005 for the definition). It is important to note the relationship and approach to the determination of Eb that is taken for any given AMS data set. Generally CE ~ 0.5 works well for most ambient particles, and deviations from that rule can be estimated from the composition of the aerosol (see Middlebrook et al., AS&T, 2012 for further details).
- The use of the CV is starting to generalize, and may significantly improve the accuracy of AMS measurements, by eliminating (or greatly reducing) the uncertainties due to CE. This will also allow more precise identification and quantification of other sources of uncertainty, or of instrument problems (of the AMS, or just as often of the instruments that the AMS is compared to) that are sometimes "disguised" as anomalous values of CE.
- The AMS mass concentration precision at low concentrations is the same as the detection limits. These have historically been defined by considering the variability in measurements during filter periods, and more recently using the continuous approach detailed by Drewnick et al. AMT 2009. Precision at higher concentrations (a few percent) is much better than the accuracy (several tens of percent).
What are the uncertainties on the quantification of OA due to its relative ionization efficiency?
- A recent publication presents a simple theoretical model that predicts a molecular weight-dependent effect on the ionization efficiency of molecules detected by the AMS, which is not accounted for explicitly in the standard AMS quantification methods. A response was published by several AMS users that states that and other effects are implicitly included in AMS calibrations, and presents a range of evidence demonstrating that the predictions of large errors on OA quantification made with the theoretical model are inconsistent with observations. Real uncertainties are consistent with the stated uncertainty of AMS OA measurements (+/-38% accuracy, see above).
- A model that describes the complete AMS detection process and reproduces the experimental observations is not available at present. Incomplete models, although they can be useful in guiding characterization work, should not be used to draw conclusions about the performance of real instruments.
- Specific calibrations have always been strongly recommended when working with pure organic compounds or simple mixtures in the lab, or when analyzing specific OA sources, and that is the individual responsibility of each user group, as reiterated in the response from the AMS Users.
Data Averaging FAQs
How do I properly average AMS products to longer timescales?
- Typically the AMS reports 2 types of scalar products:
- Aerosol concentrations (OA, sulfate, nitrate, ammonium and chloride), which are extensive properties,
- Intensive properties (calculated as ratios of extensive properties) that can be used to describe the chemical evolution of the aerosol in more detail. A common example is the O:C ratio of OA. A detailed list of intensive variables reported by our group can be found bellow
- For averaging extensive properties (concentrations), simple arithmetic averaging is used. For averaging intensive properties, they need to be weighted by the aerosol concentration variable that is in the denominator. For example if two data points are averaged that have OA = 10 ug m-3 and O:C = 1 and OA = 0.1 ug m-3 and O:C = 0, simple arithmetic averaging would result in an O:C = 0.5, when the correct answer is O:C ~1. (In detail it is slightly more complicated, see the next section).
- Note that for aircraft datasets, the intensive properties are only reported for data points above the detection limit of the relevant aerosol species.
- The weighted average should be calculated as follows:
Average(fvar) = Sum(fVari * wVari) / Sum(wVari)
- where fvar is the fractional variable and wVar is the weighting variable.
- As an example, to average 1 s data for the fraction of OA at m/z 44 (f44) to higher time resolutions, this would translate into:
Average(f44) =Sum(f44,i * OAi) / Sum(OAi)
- For averaging OA elemental variables (O:C, H:C OA:OC and OSc), weighting by OA is not appropriate; please find the correct averaging procedure below.
- For averaging aircraft data, special consideration has to be given to the exact match of AMS data reporting interval and the time grid you are trying to regrid to. Please refer to the discussion in the aircraft specific section.
How do I average OA elemental composition variables (O:C, H:C OA:OC and OSc)?
- The elemental ratios O:C and H:C should be recalculated after averaging the underlying elemental masses for organic carbon (OCtot), hydrogen (Htot) and oxygen (Otot). This can be done using the reported O:C and H:C ratios, as well as the reported OA:OC ratio (Aiken et al., 2008):
OCtot = OA / (OA/OC)
Otot = OCtot * O/C *16/12
Htot = OCtot * H/C *1/12
- As an example, given an OA concentration of 10 ug/m3, an OA:OC ratio of 2, O:C of 0.64 and H:C of 1.4, one would calculate 5 ug/sm3 of organic carbon (OCtot), 4.3 ug/sm3 of organic oxygen (Otot) and 0.6 ug/sm3 (Htot); the 0.2 ug/sm3 “unaccounted” OA mass in this example is comprised of heteroatoms such as N and S, but does not matter for this calculation.
- These three quantities, OCtot, Htot, and Otot, as well as total OA should be calculated at the original time resolution and then averaged to the interval(s) of interest. Then, the atomic ratios can be calculated straight from their definitions:
Average(O:C) = Average(Otot) / Ave(OCtot)*12/16
Average(H:C) = Average(Htot) / Ave(OCtot)*12/1
Average(OA:OC) = Average(OA) / Ave(OCtot)
- Likewise, average carbon oxidation state of OA (OSc) can be estimated from the following approximation (Kroll et al, 2011):
Average(OSc) = 2 * Average(O:C) - Average(H:C)
Sizing FAQs
What is the diameter measured by the AMS?
- The AMS measures vacuum aerodynamic diameter (dva, see DeCarlo et al. AS&T 2004), which is proportional to particle density, and decreases with increasing dynamic shape factor for non-spherical particles. Note that dva is DIFFERENT from the traditional definition of aerodynamic diameter (da) which is proportional to the square root of the particle density and also has a different dependence on particle shape factor (see DeCarlo et al. 2004 for details).
Does the measured diameter change if the particles are dry or wet?
- dva depends on the particle density. As shown in Appendix B of DeCarlo et al. (2004) for mixed organic/inorganic ambient particles with densities around 1.5 g cm-3, the effect of adding water on the particle dva is surprisingly small. This is by chance, as the increase in particle diameter closely compensates the decrease in particle density. This also assumes that the particles stay spherical after drying.
- Also note that the particles lose a lot of water (of the order of 3/4 to all the water, depending on various details) when entering the AMS vacuum system, see e.g. Zelenyuk et al., 2006.
- For other situations, the theoretical formulations of DeCarlo et al. (2004) can be used to predict the changes of dva due to water uptake or drying.
How can a sensible averaging time for AMS Size distributions be estimated?
While size-segregated AMS data is not fundamentally different from total MS data, the duty cycles are typically significantly lower both due to the inherent duty cycle of the chopper wheel used to acquire size distributions and the fact that most AMS practitioners spend less time acquiring in size-segregated mode. Hence the (species-dependent) detection limit for size segregated data can be easily derived from the MS detection limits (see above) by just applying the SD mode duty cycle (both for the chopper wheel, e.g. for how long does the chopper transmit particles, and for the acquisition, e.g. how long is size segregated data acquired vs total mass mode) to the AMS detection limits.
DL(Species X, SD Total) = DL(Species X, MS Total)/sqrt(Dutycycle(Chopper Wheel)*Dutycycle(SD Mode)/Dutycycle(MS Mode))
In most ground studies, Dutycycle(SD Mode)/Dutycycle(MS Mode) ~ 0.2. For the typical operation of the CU AMS aircraft, it's ~0.1. The mass duty cycle of the chopper wheel is either ~2 (4% for aircraft studies) if it was obtained in single slit/"regular PToF" mode (please check the data header or inquire with the data provider to confirm this detail) or ~50% (for multislit, "ePToF" mode). So taken together, that means that to get the same detection limit as in MS mode, for ground data one would have to average 3x longer (ePToF) or 16x longer (regular PToF), while for the aircraft data it would be 4.5x (ePToF) and 16x (PToF)
The DL discussed above describes the amount of mass needed to get a valid mass spectrum if you sum up all size channels and hence is considerably lower than what is needed to get a good signal for a full 40-60 channel AMS SD. One obvious criterium is to make sure that the integral of the size distribution gives physically meaningful species concentrations, as described by the normalization factor (SD integral to total SD ratio) that is reported in the CU AMS data files. Based on the ATom analysis (ePToF, 20 size channels per decade, which is a reasonable value both in terms of intrinsic resolution and noisy reduction), to get sensible values (so no negatives and no crazy positive values either), one needs about 6-15x DL(Species X, SD Total), depending on Species X. Using an average factor of 10x, that would translate into integration times 30x longer (ePToF ground), 160x longer (PToF ground+aircraft), 45x longer (ePToF aircraft)
The above values will provide an interpretable, but still very noisy size distribution, so for robust, presentation-ready plots 3-4x higher averaging times are typically needed, so about 120x (ePToF ground), 640x (PToF ground) and 180x longer (ePToF aircraft). By way of example, for a purely organic ambient aerosol distribution assuming a CE~0.5 and an average concentration of 10 ug sm-3, that would mean:
- For ground studies, using the DL from deCarlo et al, 2006 (~ 50 ng m-3 at CE=1 for 1 min averaging), 12 min (ePToF) or 64 min (PToF) averaging
- For aircraft studies, using the DL from Guo et al, 2021 (~80 ng sm-3 at CE=1 for 1 min averaging), 23 min (ePToF) or 81 min (PToF) averaging
These values scale with sqrt(N), so for an average OA concentration of 1 ug m-3 this values need to be trippled.
Size Range FAQs
What is the size cut of AMS measurements?
- The transmission of particles through the AMS aerodynamic lens changes as a function of size, and is dependent both on the geometry of the critical orifice upstream of the lens, the lens in question, and the lens pressure.
- Transmission through the standard AMS lens into a collimated beam that reaches the vaporizer falls to zero at around 35 nm dva (Zhang et al., ES&T 2004), although it depends on the particular instrument and lens pressure.
- At the large end, the decline in transmission is not as sharp, falling off at around a micron, depending on operating pressure. Hence the AMS is often referred to as an approximately PM1 instrument. Details on the aerodynamic lens and/or transmission curves can be found in Jayne et al., AS&T 2000; Zhang et al., AS&T 2004; Liu et al., AS&T 2007; Takegawa et al., AS&T 2009; Bahreini et al. AS&T 2008; and Hu et al. 2017 (Fig S2). There is some variation between specific aerodynamic lenses in different instruments as evidenced by comparing those papers. In particular the lens tested in Liu et al. (2007) suffers from a degradation in transmission at the high sizes that has been observed a few other times, for unclear causes, but it should NOT be considered the default for AMS measurements.
- Note that the size cut of the AMS (vs. dva) is similar to that of typical PM1 cyclones (vs dta). There is a lot of confusion in that some people think that "PM1" means complete transmission of everything smaller than 1 um, but that is not how the terms "PMx" are used in the aerosol community. The number after "PM" corresponds to the diameter of approximately 50% transmision.
- See an approximate transmission curve for model or instrument intercomparison purposes below.
- If a particular AMS is operated at too low lens pressure the transmission of larger particles can be seriously degraded (see Zhang et al. AS&T 2004 and Bahreini et al. AS&T 2008). Another reason for lower than normal transmission is poor alignment of the aerodynamic lens, which has been a problem for some groups and campaigns.
What size range should be used to compare models or other measurements to the AMS?
- An approximate transmission curve to be implemented in a model, would involve first converting the model distributions to dva (typically assuming internal mixing). This requires determining the average density at each particle size. See [1] for details about how to estimate the density.
- Then the following approximate transmission curve should be used, which is an average of those in the studies above (as reported in Appendix B of Knote et al., 2011, with the high end made more accurate based on the Hu et al. 2017 (Fig. S2) and other measurements):
- 0% transmission below 40 nm dva
- linear increase in transmission vs log(dva), from 0% at dva = 40 nm to 100% at dva = 100 nm
- 100% transmission from dva = 100 nm up to dva = 550 nm
- linear decrease in transmission vs log(dva), from 100% at 550 nm to 0% at dva = 1.5 um
(If a specific measurement of the transmission efficiency of the AMS(s) used in that study is available, then that curve could be used instead. However the transmission curve is remarkably difficult to measure accurately, especially for inexperienced users, and it is easy to make large errors. So unless you have high confidence and have double-checked your measurements, you may be better off using the above curve).
- The following paragraph from Fast et al. (ACP 2009) summarizes this issue well, although it would have been preferable to use the approximate transmission curve above:
- "The size cut of the particles that can be measured by the AMS is reported to be 1 μm in vacuum aerodynamic diameter (PM1 in dva) (e.g. Canagaratna et al., 2007). This size cut corresponds to slightly smaller particles than the 1 μm cut in transition-regime aerodynamic diameter (dta) that is typically used to define PM1 ambient measurements using cyclone or impactor inlets operated at ambient pressure, with the exact correspondence being dependent on ambient pressure and on particle density and shape and thus composition (DeCarlo et al., 2004). For example, for the average density of 1.4 g cm−3 calculated from the chemical composition measurements at T0 or CENICA [in Mexico City] (Aiken et al., 2008a; Salcedo et al., 2006) and the pressure of Mexico City, a PM1 cut in dva corresponds to a PM0.9 cut in dta. There can be some variation in individual aerodynamic lenses as well, which in some cases lead to smaller size cuts (Liu et al.,2007). The PM1 cut in dva corresponds to 0.7 μm physical diameter [for spherical particles] under the average conditions in Mexico City. Therefore, only predicted organic aerosols from the four size bins [in the model] below 0.7 μm were used to compare with the AMS measurements."
Density FAQs
Can I estimate the material density from the AMS composition measurements?
- Yes. This requires a few assumptions:
- The particles are internally mixed (at all sizes if calculating a bulk density, or at each size if calculating size-resolved density)
- Refractory species either represent a small fraction of the mass, or their concentrations have also been measured by other methods.
- The volume of the different species is additive. This is typically a good approximation.
- Under those assumptions, you can estimate the material density of the particles by using Equation 4 of DeCarlo et al., 2004 or the (perhaps clearer) Equation 2 in Salcedo et al. 2006
- The densities of individual species are needed to do the calculation. For these we recommend:
- 1.78 g cm-3 for ammonium sulfate (CRC handbook)
- 1.72 g cm-3 for ammonium nitrate (CRC handbook)
- 1.52 g cm-3 for ammonium chloride (CRC handbook)
- 1.0 g cm-3 for hydrocarbon-like OA (HOA, i.e. primary combustion organics such as vehicle emissions)
- For SOA or biomass-burning dominated organics the density depends on O/C (see below) and typical values are 1.25-1.45 (Cross et al. (2007); Vaden et al. (2011); Kuwata et al., 2012). When high-resolution and elemental analysis of OA are available, or by estimating O/C from f44 (per Aiken et al., 2008), the density of OA can be estimated from its composition according to the procedure in Kuwata et al., 2012.
- 1.77 g cm-3 for black carbon (Park et al. 2004)
- dust and metals ~ 2
- sea salt = 2.2 g cm-3 (Lewis and Schwartz (2006))
- This calculation can be made in a size-resolved manner, e.g. see Figures 4 and 8 in Zhang et al., 2005.
Can I estimate the effective density from combining SMPS and AMS measurements?
- Yes, and this has been done in many studies. Note that the effective density only equals the material density for spherical particles (without internal voids). See equation 37 and associated text in DeCarlo et al., 2004 for the details of the procedure.
- Do note that there are different definitions of "effective density" in the literature, which give different numerical values for the same particles. See Figure 6 of DeCarlo et al., 2004 and associated text for further details.
PMF FAQs
Can PMF be applied to aircraft datasets?
PMF can be successfully applied to aircraft datasets, e.g. see Marais et al., 2106 which reports IEPOX-SOA from PMF of the CU aircraft AMS dataset from the SEAC4RS campaign, or Hodshire et al. (2019), that reports extracting MSA from the remote ATom dataset. Primary OA (POA) can be extracted for aircraft studies close to sources, see e.g. Nault et al., 2018 for the KORUS-AQ aircraft campaign. However POA can be a more difficult problem for remote datasets, see below.
Why can't you always extract POA through PMF of aircraft datasets?
(The text below is adapted from Hodzic et al., 2020).
For studies close to sources (e.g., Jimenez et al., 2009), positive matrix factorization of AMS mass spectra (PMF; Ulbrich et al., 2009) can be used to estimate the contribution of primary sources (mostly from transportation, heating, cooking, and biomass burning) to total OA. This approach is not suitable for remote aircraft datasets (such as the ATom campaigns). To accurately resolve a minor factor such as POA in a remote AMS dataset, there needs to be a combination of
- (a) sufficient OA mass concentration so that the signal-to-noise ratio of the spectra is sufficient;
- (b) enough fractional mass for the factor to be resolved (> 5% in urban areas per Ulbrich et al., 2009; probably a larger fraction at low concentrations such as in ATom);
- (c) sufficient spatiotemporal variability (“contrast”) in the relative contributions of different factors, since that is part of what PMF uses to extract the factors;
- (d) sufficient difference in the spectra of the different factors (for the same reason as c); and
- (e) relatively invariant spectra for each factor across the dataset (as this is a key assumption of the PMF algorithm).
As an example of a nearly ideal case, in Hodshire et al. (2019) we extracted MSA by PMF from the ATom-1 data and were able to match that factor with our independently calibrated MSA species. A very distinct and nearly invariant mass spectrum was measured repeatedly near sources (MBL) and was mostly absent elsewhere, thus providing strong spatiotemporal contrast) and accounted for about 6% of the fractional mass and 15% of the variance in time. Thus, all the conditions were met. For POA, on the other hand, the air sampled in ATom and coming from, e.g., Asia has POA and SOA very well mixed, with little change in their relative mass fractions vs. time (as the aircraft flies through that air mass). POA is very low, as documented in Hodzic et al., 2020. Atmospheric aging makes the spectra from all OA sources more and more similar as measured by AMS spectra (Jimenez et al., 2009). Thus, most of the conditions above are not satisfied for extracting POA by PMF analysis of this dataset.
FAQs specific to Jimenez Group Aircraft Data
I am using AMS data from the Jimenez Group from a data merge generated by NASA (or others). Are there any issues I should be aware of?
- YES! First of all the data headers are lost in the merges. You will want to look at the headers in our original datafiles for critical information on the instrument and how to interpret the different variables. We put a lot of effort into keeping those headers up-to-date. See also the next question.
Should I use the merged data for intensive properties such as O/C?
- Only with caution and comparing against our reported values. Also, as of Dec. 2016, ALL public merges that we are aware of (including the ones from NASA, and also from Steve Wofsy for ATOM) merge intensive properties INCORRECTLY. They are merged as straight averages, while the correct way is to merge weighed averages (details here). This affects all intensive properties such as O/C, H/C, OM/OC, estimated density, f44, f57, f60, f82, estimated pH and some others.
Should I do my own averages of your 1 s data for averages of 1 min or longer?
- NO! Our group reports aircraft data at two native time resolutions, 1 s and 1 min. These are in fact very different products, since the 1 min data is computed by averaging the native 1 s raw spectral data and fitting the mass spectra at higher S/N in a completely separate datastream.
- The 1 s AMS data, on the other hand, is a combined product: Concentrations are reported at 1 s time resolution (by analysis of the raw 1 s data), while intensive properties are typically also reported at 1 s resolution, but replaced with the more robust 1 min data when the weighting variable is very close to the detection limit. As of this writing (Sep 2016), for OA intensive properties, any data below 1 ug/sm3 OA (with CE of 1) is replaced with 1 min data.
- Hence, the 1 min product is BETTER than just averaging the 1 s product. So always use the 1 min product if you work at that time resolution or lower.
What are the typical AMS-measured intensive properties reported by our group and their weighting variables?
- Here is the list of fractional products that our group currently reports (as of Dec 2016), with the corresponding weight variable:
- AmmBalance_lt_1um_AMS (and estimated pH, when reported): Weighted by sum of moles: (mNO3+mSO4+mChl), so (NO3/62+SO4/48+Chl/35.5), where NO3, SO4, and Chl are the mass concentrations reported.
- Density_lt_1um_AMS: Weighted by total aerosol mass: (OA+NO3+NH4+SO4+Chl)
- f43_lt_1um_AMS, f44_lt_1um_AMS, f57_lt_1um_AMS, f60_lt_1um_AMS, f82_lt_1um_AMS, f91_lt_1um_AMS, fC2H3O_lt_1um_AMS, fCO2_lt_1um_AMS, fC4H9_lt_1um_AMS, fC2H4O2_lt_1um_AMS, fC5H6O_lt_1um_AMS, fC7H7_lt_1um_AMS: Weighted by OA mass concentration.
- OrgNitr_Fraction_lt_1um_AMS: Weighted by NO3 mass concentration.
What aircraft dataset should I use for calculating AMS variable averages?
- For averaging to time intervals <1 minute, use the 1 s reported dataset. When averaging AMS data to time intervals >1 minute, especially in clean conditions, it is strongly recommended to use the 1 min data whenever possible. In cases where the averaging time interval is >1 min, but does not fit the 1 min cycle, it is recommended to still use 1 min data from the first to last full minute and 1 s data for the fractional minutes at the beginning and end. For correct results, when averaging both 1 s and 1 min data it is important to weight the later by the actual measurement time per 1 min cycle (TOpen), reported in the ICARTT header. As of this writing (Nov 2016), TOpen is normally 46 s.
- As an example, if one were to average AMS data to a time scale consisting of 3 min intervals, starting at 30 s past the minute, the correct average for OA (extensive property) would be:
Ave(OA, 00:00:30-00:03:30) = Sum(OA_1s, 00:00:30-00:00:59)/46 + Sum(OA_1min, 00:01:00-00:03:00)/2 + Sum(OA_1s, 00:03:01-00:03:30)/46
- So use division by TOpen (46 s) to properly average and weight the 1 s data in the fractional full minutes, and do a straight average of the 1 min data for the full minutes.
- To average an intensive property, such as f44, according to the expression given above:
Average(f44) = Sum(f44,i*OAi) / Sum(OAi),
- both Sum(OAi) and Sum(f44,i*OAi) should be calculated, as above, weighting by TOpen as appropriate, and then Average(f44) can be calculated.
How can I estimate the detection limits for my averaged data (aircraft only)?
- If you are averaging multiples of 1 min, you can estimate the detection limit for a given species by using:
DL(Species X, N minutes) = DL(Species X, 1 minute) / sqrt(N)
- This is basically identical to the normal AMS acquisition case, where DLs also scale linearly with sqrt(time interval).
- On the other hand, if you are averaging 1 s data up to 1 min, the correct equation (accounting for the different times spent taking ambient data vs background, TBack):
DL(Species X, N seconds) = DL(Species X, 1 s) *sqrt( (1+TBack/N) / (1+TBack) )
- TBack can be found in the ICARTT header, it typically is 6 s.
How does flying through clouds affect the data reported by the aircraft AMS?
- Clouds transects, particularly through ice clouds, present a challenge to any aircraft instrument measuring aerosols since some of the liquid/solid water particles will impact on the inlet and lead to both ablation of the inlet surface itself or material deposited on the inlet walls (Weber et al., 1998, Murphy et al., 2004). The problem is known to be worse for ice clouds. Most of the ablated material from the inlet walls tends to be refractory (metals and soot) and hence the AMS does not detect those. This contrasts with large artifacts seen on particle counters and laser-ablation single particle instruments, which do detect refractory particles. Some ablated material, however, could be organic (likely deposited during a previous boundary layer transect).
- Measurements in heavy ice clouds during previous campaigns (in particular DC3 in 2012) show that the AMS only observed very infrequent spikes in OA (once every 60-90 s or so), during periods in which other instruments were seeing large inlet artifacts, that were likely related to this issue. In most cases, these spikes are associated with either unusually high particulate water (pH2O) or zinc (the latter is believed to originate from the inlet anodized coating). A “cloud flag” is provided in the reported data files that flags individual 1 s points if either of these parameters (pH2O and Zn) are above an empirically determined threshold. Care should be exercised when using AMS data during periods with a high number of non-zero cloud flags, and it is recommended to contact the AMS data manager for additional guidance.
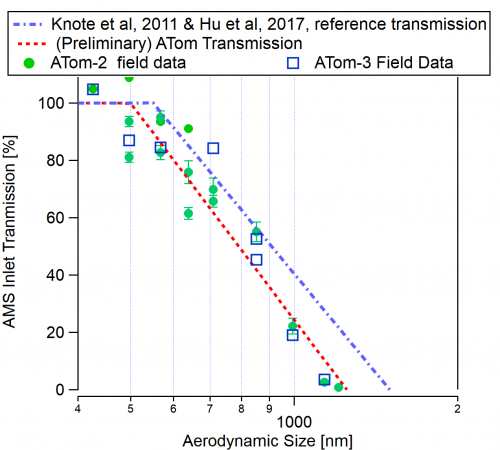
Is the size transmission the same for the CU Aircraft AMS than for the standard AMS?
- The standard AMS transmission is discussed in this section above.
- For aircraft AMS, normally a pressure-controlled (PCI) inlet is used. If no PCI is used, there are major changes to the size calibration and the transmitted size ranges as ambient pressure changes with altitude during the flight.
- For planes that fly at lower altitudes, the PCI volume can be operated at higher pressures, and the transmission is similar to the default one.
- For planes such as the DC8 where very high altitudes (40,000 ft) are reached, the PCI has to operate at much lower pressures, which leads to slightly worse transmission at the higher end. See the graph below for a comparison of the standard transmission with preliminary data from the ATOM campaign.