), and 
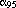using
Fisher statistics. As described in the Statistics section, directions
and statistics obtained with approximations produce a beep (up to 4 beeps for a
Least Squares Equal Area plot and 6 for the Locality Equal Area plot). The
Plot Error Ellipse option becomes active once the Fisher Stats option is
selected; when checked, the 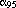cone of confidence is plotted. The
"Hemisphere" option is identical to the "Fisher Stats" above except that points
in opposite hemispheres are inverted; this produces a Fisher mean of reversed
and normal polarities inverted through the origin so that they can be combined.
More details are in the Statistics section. When the "Elliptical statistics"
option is selected, either the Bingham or the Non-Parametric Statistic can be
used; one or the other will be checked. Bingham uses Bingham
statistics. Note that this uses a lookup table and approximations for the
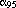construction of the estimates that are probably unreliable for data
distributed in a girdle (plane data). "Non-Parametric Stats" uses
non-parametric statistics suggested by Watson as presented in Fisher et al.
(1987) (thus the label "Watson" when the statistic is displayed). This
statistic becomes more accurate with larger numbers of directions; the
uncertainty ellipses are probably unreliable with under about 20 samples.
"Plot Girdle" plots the girdle to the confidence ellipse (the ellipse plus and
minus 90°ree;). This might be desired if you had a group of plane or circle
fits that all clustered near each other and you wished to plot the region where
the two magnetization components would lie.
One of the three options below is always checked when the "Elliptical stats" option is active:
- Use as Lines: Assume all the plotted data represent line fits (i.e., are drawn from a bipolar distribution). Thus apply bipolar forms of the elliptical statistics to the data.
- Use as Planes: Assume all points represent plane or circle fits (i.e., drawn from a girdle distribution). Thus apply the girdle forms of the elliptical statistics (which produces the pole to the plane that best fits the data).
- Combine Lines plus Planes: Only available in the Least Squares Equal Area plot. As described below in the Statistics section, combine line and plane fits to get the best estimate of the desired magnetization component.
- Use as Lines: All data shown will be assumed to represent line data (i.e., drawn from either a Fisher or a Fisher "Hemisphere" distribution)
- Combine Lines and Planes: (least squares only): Using the formulation of McFadden and McElhinny (1988) to combine line and plane or circle fits. This is discussed a bit more in the Statistics section. When this is selected, the "Use arc constraints" button is active; when checked, this restricts the points along plane or circle fits used to those along the arcs from about the last point used to about the antipode of the first point used (see the diagram in the description of the .lsq file format in the Formats section).
